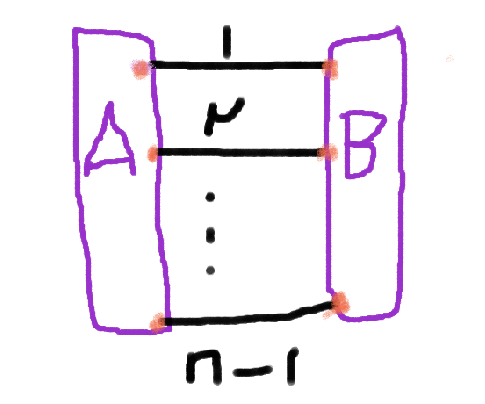
ببین راه حل درسته :ابتدا با برهان خلف ثابت می کنیم که گراف هیچ یال برشی ندارد -سپس استقرا می زنیم روی n و یک تطابق کامل از یک رنگ را حذف می کنیم حال هر مولفه همبند هستش وبه هر مولفه 2 تا از این رنگ انتخاب شده وصل است
2015-04-26 04:39:02 -0500 دمرلسلام میدونستید انجمن علمی نخبگان دانشگاه صنعتی شریف مسابقه تخصصی مهارت سنجی برنامه نویسی و داده کاوی گذاشته است آدرس سایتش www.fanavard.com
2015-08-06 09:55:26 -0500 امیر شکریسلام میگم یک سر به سایت www.fanavard.ir بزنید. مسابقات برنامه نویسی شون شروع شده. گواهی رسمی از طرف دانشگاه شریف می ده. 50 تا سکه هم جایزشه
2016-10-26 11:07:41 -0500 امیر شکری