متاسفانه بنده قادر بدین کار نیستم. تئوری را دو ماه نخوانده و و فراموش نموده ام. و بدین سان ذهنی آماده مرا یاری نخواهد کرد...
2015-07-28 11:37:58 -0600 سی پلاس پلاسآمار پرسش:
- پرسیده شده: 2015-07-27 23:34:33 -0600
- مشاهده شده: 409 بار
- بروز شده: 2015-08-05 10:08:09 -0600
پرسش‌های مشابه:
پیدا کردن گراف دوبخشی کامل یکرنگ
حداکثر تعداد یال‌های گراف بدون مثلث
اثبات همبند بودن مکمل گراف ناهمبند
همه را با تلفن خبر کنید - دوره ی 05 - مرحله ی 1
رنگ‌آمیزی صفحه بخش‌بندی شده توسط دایره‌ها با دو رنگ
پیدا کردن مولفه های قویا همبند گراف جهت دار
انگور، آن هم از نوع «درختی» - آزمون دوم آزمایشی شاززز
نکاتی در مورد نوشتن پاسخ:
استفاده از ویرایشگر:
علائم ریاضی:
در گراف دوبخشی با 3n-2 یال ؛ حداقل یک مربع وجود دارد
سلام.
اثبات کنید در گراف دوبخشی با 3n-2 یال ؛ حداقل یک مربع(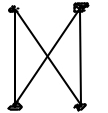
) وجود دارد .
2015-07-27 23:34:33 -0600
آرپا 947 ● 13 ● 15 ● 31
نظرات
1 پاسخ
راه حل غلطه! با تشکر از آقای کاملی برای گفتن مشکل راه حل :)
اولا سوالت غلطه. (چون اگه نگی گراف مورد نظر باید ساده باشه مثال نقض داری)
دوما: گرافمون حداقل یه دور داره، اگه درجه همه راس هاش بیشتر یا مساوی ۲ باشن همتون احتمالا بلدین که دور وجود داره، اگر نه هم یه راس با درجه ۰ یا ۱ رو بکن، استقرا بزن رو n با فرض داشتن حداقل اونقدر یال، و ثابت میشه.
حالا اگه گراف دور ۴راسی داشته باشه، وسط اون دوره یال وجود نداره(اگه داشته باشه دور فرد ایجاد میشه و گراف دوبخشی نیست)، پس کافیه ثابت کنیم گرافمون دور ۴راسی داره.
حالا میایم استقرا میزنیم رو n: فرض خلف میکنیم که کوتاه ترین دور، حداقل ۶راس داره. یه کوچکترین دور رو میگیریم. وسط این دوره یال نیست، اگه بود دور کوتاه تر بجود میومد. از این دور به هر راس خارج از این دور حداکثر یه یال وصله، اگه بیشتر باشه یه دور کوچک تر ایجاد میشه. طول این دور رو میگیریم k. پس حداکثر k + (n - k) q یال به این دور وصله که میشه n تا. حالا اینا رو میکنیم، هنوز شرط مسیله برقراره( پس دقت کنید که بیش از ۴ تا راس تو گراف میمونه، چون شرط سوال برای گراف های زیر ۵ راس برقرار نیست ). حالا طبق فرض استقرا، یه دور ۴راسی وجود داره، پس فرض خلف باطل و حکم صحیح است.
2015-07-29 11:43:44 -0600
فارسی 99 ● 4
نظرات
آخرش رو من نفهمیدم...چجوری طبق فرض استقرا یه دور 4 راسی داریم؟...بعدشم اینکه شما اول باید بگین فرض خلف باطل میشه پس یه دور 4 راسی داریم...ولی شما گفتین یه دور 4 راسی داریم پس فرض خلف باطله؟خب از کجا اوردین که دور 4 راسی داریم؟...شاید من خوب متوجه نشدم
2015-07-29 12:27:33 -0600 تنیسونخوب اومده اون راس دور‌ها و اونایی که به این دور وصل هستن رو حذف کرده، گفته حالا توی گراف جدید هنوز شرایط مسئله برقراره، و پس از فرض استقرا کمک گرفته دیگه :)
2015-07-29 13:03:20 -0600 توفیقی❊تنیسون خب قبول داری اگه بتونم یه جور دیگه ثابت کنم که دور ۴راسی داریم، فرض خلفی که میگه دور ۴راسی نداریم باطل میشه؟؟ من دقیقا همین کارو کردم. اینکه دوره ۴راسی داریم هم با استقرا گفتم دیگه، یه سری راس رو حذف کردم، ثابت کردم یال هایی که با حذف اونا میمونن، از اون مقداری که میخوایم کمتر نیست.
2015-07-29 13:52:14 -0600 فارسی