سلام میگم دیگه !

جواب : $\mathbf{\left \lceil log(n) \right \rceil}$

اثبات وجودی :استقرا میزنیم :

پایه : برای $n=3$ کافی است رنگ دو یال را از نوع 1 و یال سوم را از نوع 2 قرار دهیم .

فرض : برای $n=k-1$ راس درست است.

حکم :برای $k$ نیز درست است .

ابتدا گراف رو به دو دسته $\left \lfloor \frac{k}{2} \right \rfloor$ و $\left \lceil \frac{k}{2} \right \rceil$ تقسیم میکنیم و یال های بین این دو دسته را از نوع رنگ 1 قرار میدهیم . حال هر دسته رو طبق استقرا مون درست میکنیم بعد عدد رنگ یال توی هر دسته رو یکی زیاد میکنیم . حالا بازم شرایط مساله دست نخوره است پس این با این جواب میتونیم یه گراف بسازیم که شرایط مساله تغییر نکنه .

اثبات بهینگی :

لم 1 : برای هر گراف با شرایط فوق (مساله) اگر فقط یال های یک رنگ رو تو گراف بزاریم گراف حاصل دوبخشیه .

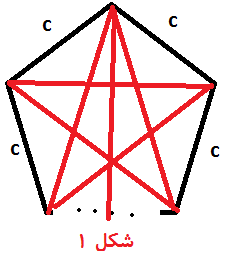
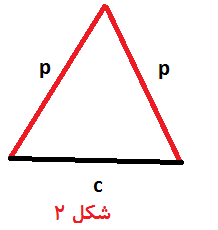
اثبات لم : طبیعتا اگر گراف رو با یال های یک رنگ مانند $c$ درست کنیم مثلث نداره . حالا برهان خلف میزنیم یعنی فرض کن دو بخشی نباشه پس یه دور فرد داره .کوچیکترین دور فرد اونو بگیر قطعا یال های بین رئوس غیر مجاور این دور از $c$ بیشتر اند (شکل 1) حالا یه مثلث رو بگیر که یک یالش یکی از اضلاع دور باشه و یال های دیگش قطر دور باشه .(شکل 2) عدد دو یال قطری آن برابر و بزرگ تر از $c$ اند پس به تناقض میرسیم پس فرض خلف باطل و حکم برقرار است .

خب حالا میریم سره اثبات کلی : دوباره برهان خلف میزنیم فرض کنیم رنگ آمیزی بهینه تری وجود داشته باشه (فرض کنید با $ \alpha $ رنگ ) حالا بیاید برای هر رنگ از $\alpha $ گراف رو دو بخشی کنید (طبق لم 1) و بیاید به هر راسی یه کدی از صفر و یک به طول $\alpha $ نسبت بدید که عدد بیت $i$ ام اون نشان دهنده اینه که این راس بر اساس رنگ $i$ ام توی کدام بخش افتاده (فرض کنید بالا عدد 1 و پایین عدد 0) خب پس چون $\alpha < \left \lceil log(n) \right \rceil \Leftrightarrow 2^{\alpha} \leqslant n$ پس طبق لانه کبوتری دو راس هستند که کد های یکسانی دارند پس طبق اینکه گراف کامل است پس یال بین آن دو راس رنگ نشده است پس به تناقض رسیدیم پس فرض خلف باطل و حکم برقرار است .