به نام خدا

در یک ایستگاه قطار ریلی به شکل زیر وجود دارد: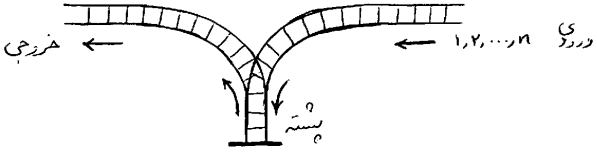

در سمت ورودی صفی از $n$ واگن با شماره‌های ۱ تا $n$ به دنبال هم و به ترتیب شماره‌هایشان قرار دارند، به طوری که واگن شماره‌ی ۱ در ابتدا و وااگن شماره‌ی $n$ در انتهای صف قرار دارند. قسمتی که در شکل پشته نامیده شده است بن‌‌بست است و واگن‌ها می‌توانند به ترتیب از ورودی وارد پشته شده و از طریق خروجی خارج شوند. پشته به اندازه‌ی کافی طولانی است و می‌تواند همه‌ی واگن‌ها را در خود جای دهد. بدیهی است که اگر تعدادی واگن به ترتیب وارد پشته شوند، قطاری که آخر وارد شده باشد اولین قطاری از این دسته است که خارج می‌شود.

نحوه‌ی حرکت واگن‌ها در این ایستگاه را با اعمال زیر می‌توان نشان داد:

$.1$عمل $I$: یک واگن از ورودی وارد پشته می‌شود.

$.2$عمل $O$: کلیه‌ی واگن‌ها موجود در پشته از آن به سمت خروجی خارج می‌شوند.

تنها اعمال فوق مجازند و توجه کنید که هیچ واگنی نمی‌تواند از خروجی به پشته و یا از پشته به ورودی بازگردد. همچنین برداشتن واگن‌ها از روی ریل مجاز نیست. با توجه به این اعمال، بدیهی است که شماره‌های واگن‌های خروجی جایگشتی از دنباله‌ی ورودی $1,2,3,...,n$ که شماره‌های واگن‌هاست، می‌باشد.

جایگشت $a_1,a_2,a_3,...,a_n$ از اعداد $1,2,3,...,n$ را دنباله‌ی قابل تولید می‌نامیم اگر بتوان آن را با استفاده از اعمال $I$ و $O$ تولید کرد. به عنوان مثال دنباله‌ی $2,1,4,3$ یک دنباله‌ی قابل تولید استو ترتیب اعمالی که این دنباله را تولید می‌کند به صورت زیر است:

1-$I$: ۱ وارد پشته می‌شود.

2-$I$: 2 وارد پشته می‌شود.

3-$O$: پشته خالی می‌شود (ابتدا ۲ و سپس ۱ از پشته خارج می‌شوند).

4-$I$: ۳ وارد پشته می‌شود.

5-$I$: 4 وارد پشته می‌شود.

6-$O$: پشته خالی می‌شود (ابتدا ۴ و سپس ۳ از پشته خارج می‌شوند).

الف) نشان دهید که آیا دنباله‌ی $2,1,3,6,4,5$ قابل تولید از دنباله‌ی $1,2,3,4,5,6$ می‌باشد یا خیر؟ دنباله‌ی $3,2,1,5,4,6$ چطور؟ در صورت مثبت بودن پاسخ، ترتیب انجام اعمال $I$ و $O$ را مشخص کنید. در غیر این صورت ادعای خود را ثابت کنید.

ب) اگر $t_n$ تعداد دنباله‌های قابل تولید از دنباله‌ی $1,2,3,...,n$ باشد، $t_n$ را به صورت یک فرمول صریح بر حسب $n$ محاسبه نمایید. (الگوریتم لازم نیست.)

ج) یک جایگشت $a_1,a_2,a_3,...,a_n$ از اعداد ۱ تا $n$ از اعداد ۱ تا $n$ داده شده است. برنامه‌ای بنویسید که مشخص کند آیا این دنباله‌ قابل تولید از دنباله‌ی $1,2,3,...,n$ است یا خیر. اعداد دنباله به ترتیب چپ به راست به صورت ورودی به برنامه‌ی شما داده می‌شود. خروجی باید در صورت قابل تولید بودن دنباله، کلمه‌ی $YES$ و سپس رشته‌ای از $I$ و $O$ باشد به طوری که با انجام این اعمال، به ترتیب، بتوان دنباله‌ی مورد نظر را تولید کرد. اگر دنباله قابل تولید نباشد خروجی برنامه‌ی شما باید کلمه‌ی $NO$ باشد.

د) در این بند فرض کنید که هر عمل $O$، خرج نمودن فقط یک واگن از پشته است (و نه تمامی آن‌ها). در این صورت اگر $S_i$ تعداد دنباله‌های قابل تولید از دنباله‌ی $1,2,3,...,i$ باشد، $s_n$ را به صورت فرمولی بر حسب $s_i$، $(i \lt n)$، محاسبه نمایید. (الگوریتم لازم نیست.)

قسمت بعدی هم اینکه $s_n$ رو به صورت یک رابطه صریح برحسب $n$ به دست بیارین.