آمار پرسش:
- پرسیده شده: 2016-04-27 10:09:51 -0500
- مشاهده شده: 839 بار
- بروز شده: 2016-04-27 12:23:48 -0500
پرسشهای مشابه:
سوال ۱ روز دوم مرحله ۲ دوره ۲۳: رشتهی نزدیک
بازی رنگی - سوال ۱ - مرحله ۲ - ۱۳۹۳
وزنهها و ماشین جادویی - سوال ۲ - مرحله ۲ - ۱۳۹۳
گاوی خسیس - سوال ۳ - مرحله ۲ - ۱۳۹۳
انتقال مهرههای گاوی - سوال ۴ - مرحله ۲ - ۱۳۹۳
یافتن کوچکترین پیچ و مهره با مقایسه آنها
دنباله و جادوگر - دوره ی 24 - مرحله ی 2
مسئله ی مسیر و شبکه - مرحله ی 2 – دوره ی 23
نکاتی در مورد نوشتن پاسخ:
استفاده از ویرایشگر:
علائم ریاضی:
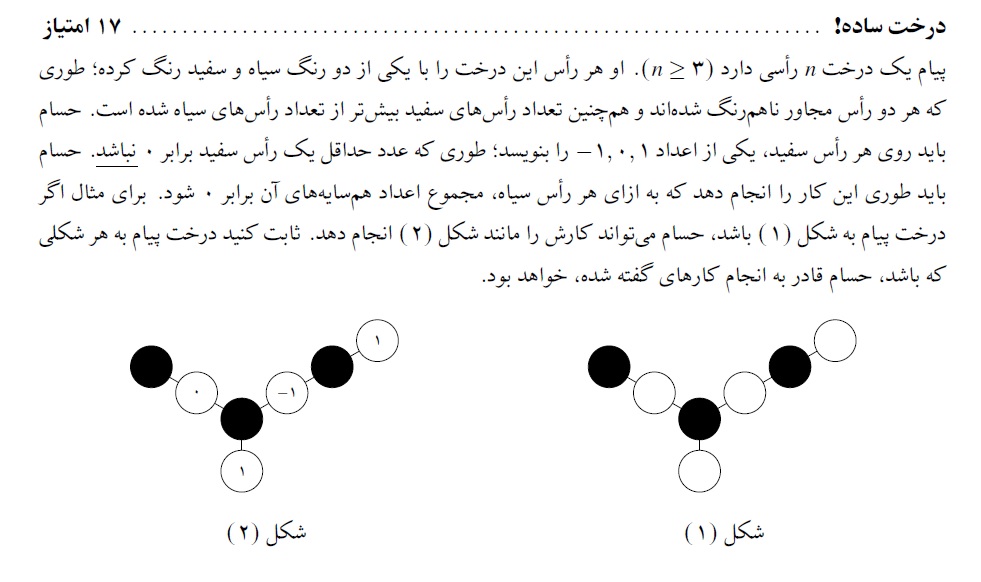
درخت ساده - مرحله ۲ سال ۱۳۹۵ - روز دوم - سوال اول
2 پاسخ
با استقرا حل می کنیم
درخت را از یه نا برگ ریشه دار می کنیم
اگر یک راس سفید که تمام بچه هایش برگ باشد داشته باشم(بچه ها سیاه اند)آن راس با بچه هایش حذف کرده(هنوز سفید> سیاه) و استقرا می
زنیم و آن راس سفید را 0 می گذاریم
اگر هم یک راس سیاه داشته باشیم که یک بچه که آن هم برگ باشد داشته باشیم باز آن ها را حذف کرده استقرا می زنیم و راس سفید حذف شده را
عددش را برابر منفی عدد راس سفید پدر راس سیاه حذف شده قرار میدهیم
حال اگر هیچ کدام از جالات بالا به وجود نیامد تمام راس های سیاه که بچه هایش برگ و سفیدند حداقل 2 بچه دارند پس دو بچه ی اول را 1 و -1 و
بقیه را صفر می گذاریمو بقیه ی سفید ها که برگ نیستند نیز سفید می کنیم
درخت رو از یه راس غیر برگ ریشه دار می کنیم.
لم) این درخت حداقل یک برگ به رنگ سفید دارد.
اثبات لم: استقرا میزنیم، برای n=1,2,3 درخت نهایی و شیوهی رنگآمیزی آن یکتا تعیین شده و حکم برقرار در آنها برقرار است. فرض میکنیم اگر $n < k$ حکم برقرار باشد و ثابت میکنیم برای $n=k$ نیز لم برقرار است.
برای اثبات از برهان خلف استفاده میکنیم، فرض کنید همهی برگها به رنگ سیاه باشد، مجموعهی همهی برگها را A و مجموعهی همهی پدر این برگهای سیاه را B مینامیم. همهی راسهای A سیاه و راسهای B سفید هستند. حال چون هر برگ دقیقا یک پدر دارد اما یک پدر میتواند پدر چند برگ باشد، پس $|A| \geq |B|$.
اگر همهی این راسها را از درخت حذف کنیم، بازهم تعداد سفید ها از سیاهها در درخت بیشتر خواهند ماند زیرا تعداد راسهای سیاه حذف شده بزرگتر یا مساوی سفیدهای حذف شده است. پس طبق فرض استقرا یکی از برگهای درخت جدید سفید است که این راس به یکی از راسهای B وصل بوده یعنی دو رنگ سفید به هم وصل بوده اند که این تناقض است. پس فرض خلف باطل و حکم ثابت است.
مسئلهی اصلی
همان طور که گفته شد طبق لم یک برگ سفید داریم که آنرا به $v$ نام گذاری میکنیم و پدر راس $v$ را با $f$ نام گذاری میکنیم. (بدیهی هست که $f$ به رنگ سیاه و تمام فرزندان $f$ به رنگ سفید اند) حال روی تعداد فرزندتان راس $f$ حالت بندی میکنیم:
حالت اول: اگر $f$ بیش از یک فرزند داشت. دو حالت داریم، یا یکی از فرزاندنش به غیر از $v$ زیردرختشان (که شامل خوب اون راس هم میشه) درش تعداد سفید ها از سیاه ها بیشتره یا نه. اگه اینجوری بود، مثلا زیر درخت راس y این ویژگی رو داشت، اون زیر درخت رو در نظر میگیریم و طبق فرض استقرا میتونیم اونو جوری شمارهگذاری کنیم که اوکی بشه، اونو شماره گذاری میکنیم، عددی که به راس y اختصاص دادیم اگه x بود، به راس v عدد -x رو اختصاص می دیم و بقیهی راسهای سفید رو ۰ میزاریم. این درسته زیرا حداقل یک غیر صفر در زیر درخت y داریم. همچنین مجموع اعداد راس f برابر با ۰ است. بقیهی راسها اگه در زیر درخت y نباشند، همهی راسهای مجاورشون ۰ هست پس ۰ هستند.
اگه چنین راسی نبود، پس هر کدوم از زیر درختا تعداد سیاه ها بزرگتر مساوی سفیدهاست پس کل زیر درخت f تعداد سیاه ها بزرگتر مساوی سفید هاست. کل زیر درخت f رو حذف میکنیم، طبق فرض استقرا بقیه رو اوکی میکنیم، حالا اگه به پدر f شمارهی x رو داده بودیم به راس v شمارهی -x رو داده و به بقیهی راسها ۰ می دیم.
حالت دوم: اگه v تنها فرزند f بود. در این صورت با حذف v و f از گراف، دقیقا یک سیاه و یک سفید کم شده، پس درخت باقی مونده شرایط رو داره پس طبق فرض استقرا میتونیم درخت باقی مانده رو عدد گذاری معتبر کنیم، حال اگه به پدر راس f عدد x رو دادیم، به راس v عدد -x رو میدیم. بقیهی راسها به غیر از f طبق فرض استقرا اوکی ان و همچنین f نیز اوکیه چون باباش x و بچهش -x عه پس در مجموع مجاوراش ۰ هستند.
پس در هر دو حالت با استفاده از فرض استقرا مسئله حل شد پس گام استقرا ثابت و حکم ثابت شد.