مطمئنین حداکثر ؟؟؟؟؟؟
فک کنم سوال این بوده :
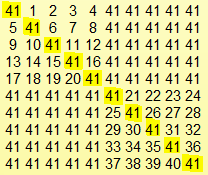
حداقل تعداد رنگ های ممکن رابیابید که بتوان خانه های جدول را به گونه ای با ان رنگ کرد که در هر سطر و ستون حداکثر 5 مختلف رنگ قرار گیرد
2014-06-29 02:54:00 -0500 هه هه ههبا ۳۷ رنگ میشه: مربع ۴ در ۴ که تقاطع ۴ سطر و ۴ ستون اول هست رو با اعداد ۱ تا ۱۶ پر میکنیم، مربع ۴ در ۴ بعدی که در تقاطع سطر و ستونهای ۵ تا ۸ هست رو با اعداد ۱۷ تا ۳۲ پر میکنیم، مربع ۲ در ۲ که در تقاطع سطروستونهای ۹و۱۰ هست رو با اعداد ۳۳ تا ۳۶، بقیه خانه ها هم عدد ۳۷ رو میگذاریم. بیشترش رو نمیدونم
2014-06-29 23:47:35 -0500 کلاه قرمزیمن با 38 رنگ تونستم فقط اثبات کمینه بودنش سخت است مثه آقای کلاه قرمزی فقط اون آخرش که می که بقیه خونه ها بهتره که خونه های سمت راست پایین رو 37 و خونه های بالا سمت چپ رو 38 و انطوری هم حکم برقراره و هم 38 رنگ
2014-06-30 00:34:25 -0500 طوفان@طوفان جان راه حل ۳۸ شما درسته؟ فکر کنم سطرها یا ستونهای وسط جدول ۶ رنگی میشن این طوری
2014-06-30 01:13:43 -0500 کلاه قرمزی