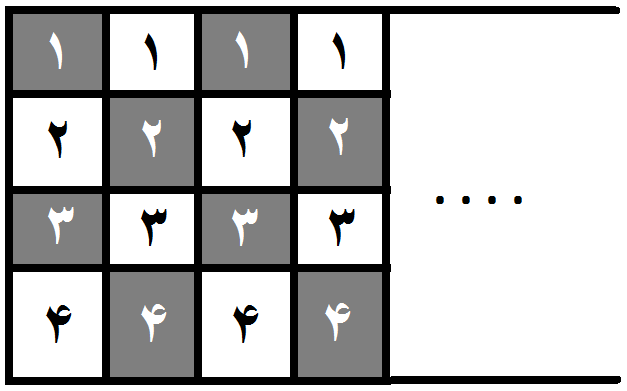
مطابق شکل بالا روی خانه های سطر اوّل عدد 1، خانه های سطر دوّم عدد 2، خانه های سطر سوّم عدد 3 و خانه های سطر چهارّم عدد 4 را می نویسیم.

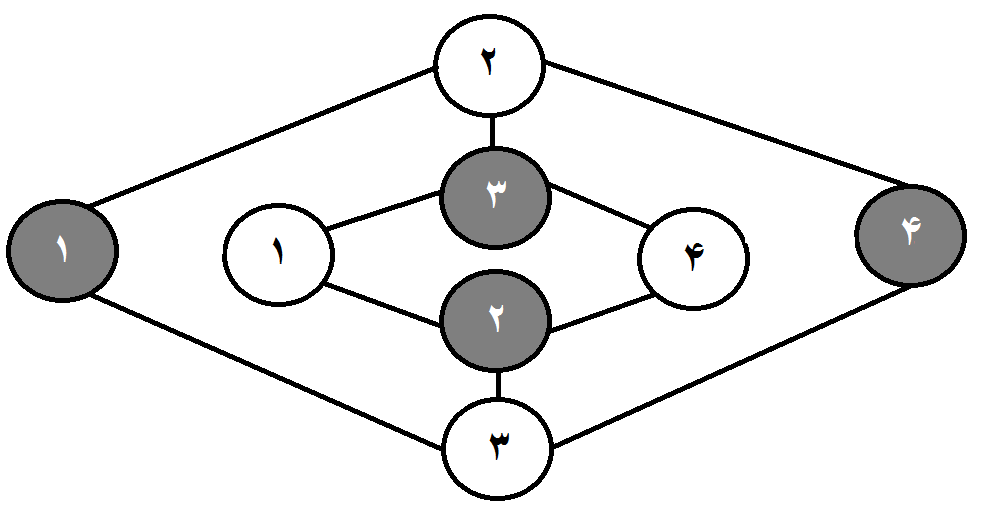
گراف حالات حرکت اسب در جدول به شکل بالاست.

در ادامه برای حالتی که خانه ی شروع یکی از خانه های {1 سیاه، 4 سیاه، 3 سفید، 2 سفید} باشد استدلال می کنیم، حالت دیگر نیز با همین استدلال و بطور مشابه اثبات می شود.

می دانیم تعداد 1 سیاه و 4 سیاه و 3 سفید و 2 سفید برابر است، بنابر این با توجّه به این که در طول حرکات هر خانه را یکبار می بینیم (خانه ای که در ابتدا در آن بوده ایم را حساب نمی کنیم.) پس این 4 خانه را هم باید تعداد مساوی بار ببینیم، اگر مدام به ترتیب همین 4 نوع خانه را ببینیم تعداد مساوی بار دیده ایم ولی 4 خانه ی دیگر {1 سفید، 4 سفید، 3 سیاه، 2 سیاه} را ندیده ایم، پس باید از یکی از خانه های 2 سفید یا 3 سفید به 3 سیاه یا 2 سیاه هم برویم تا 4 خانه ی {1 سفید، 4 سفید، 3 سیاه، 2 سیاه} هم دیده شوند. در این جا به تناقض می رسیم. (چرا؟) چون از خانه های هر عدد به تعداد برابر در جدول داریم، پس اگر مجموعه ی A را خانه های با عدد 1 و 4 در نظر بگیریم و مجموعه ی B را خانه های با عدد 2 و 3، باید بتوانیم هر عضو از B را با هر عضو از A متناظر کنیم. هر عضو را یکبار می بینیم و وقتی یک عضو از A را می بینیم، دوباره عضو دیگری از A را نمی بینیم (در گراف قابل مشاهده است) پس زمانی که از 2 سفید یا 3 سفید وارد 3 سیاه یا 2 سیاه می شویم تعداد بیشتری از خانه های B دیده ایم و از آنجایی که همانطور که گفته شد هیچ دو خانه ای از A پشت سر هم دیده نمی شوند، پس این اختلاف دیده شدن برای خانه های مجموعه ی B و A بعداً درست نمی شود، در حالی که بایستی تعداد مساوی خانه از این دو مجموعه در طول حرکات اسب دیده شود، پس امکان ندارد که بطور گفته شده مهره ی اسب خانه های جدول $4 × n$ را طی کند.