دستگاهی مانند شکل زیر را در نظر بگیرید:

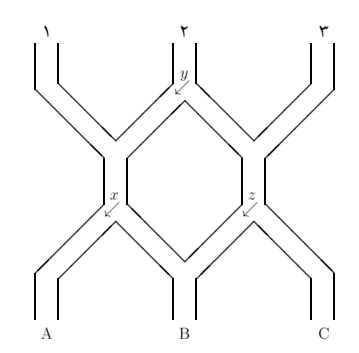
در هر یک از ورودی‌های ۱، ۲ و ۳ می‌توانیم یک گلوله بیندازیم. این گلوله به‌سوی پایین حرکت می‌کند و با توجه به وضعیت کلیدهای $x$، $y$ و $z$ از یکی از خروجی‌های $A$، $B$ یا $C$ خارج می‌شود. کلیدهای $x$ ، $y$ و $z$ به این صورت عمل می‌کنند: هر کلید می‌تواند در یکی از دو وضعیت $\searrow$ یا $\swarrow$ باشد. اگر کلید در وضعیت $\searrow$ باشد، گلوله را به سمت راست و اگر در وضعیت $\swarrow$ باشد، گلوله را به سمت چپ می‌فرستد. علاوه بر این با عبور هر گلوله از یک کلید، وضعیت آن کلید تغییر می‌کند.

در ابتدای شروع کار دستگاه، هر سه کلید در وضعیت هستند. یک دنباله مانند $a_1 a_2…a_n$({$1,2,3$}$a_i∈$ به ازای هر $i$) به‌عنوان دنباله‌ی ورودی دستگاه داده می‌شود. پس از این ابتدا یک گلوله از ورودی شماره‌ی $a_1$ ، سپس یک گلوله از ورودی شماره‌ی $a_2$ … و در انتها یک گلوله از ورودی شماره‌ی $a_n$ به درون دستگاه می‌اندازیم. فرض می‌کنیم که گلوله‌ها به ترتیب از خروجی‌های $٬b_2٬b_1$، … و$b_n$ خارج شوند ( {$A,B,C$}$b_i∈$ به ازای هر $i$) دنباله‌ی $b_1 b_2…b_n$ را دنباله‌ی خروجی دستگاه برای ورودی $a_1 a_2…a_n$ می‌نامیم.

به عنوان مثال دنباله‌ی خروجی دستگاه برای ورودی ۱۲۳۲۱، دنباله‌ی ABBCA است.

الف) الگوریتمی بنویسید که با دریافت یک دنباله‌ی ورودی، دنباله‌ی خروجی آن را پیدا کند.

ب) الگوریتمی بنویسید که با دریافت یک دنباله‌ی $s_1 s_2…s_n$ ({$A,B,C$}$s_i∈$ به ازای هر $i$) مشخص کند که آیا این دنباله می‌تواند خروجی دستگاه باشد یا خیر؟ الگوریتم شما باید سریع باشد، یعنی امتحان کردن تمام حالت‌ها مورد نظر نیست.