بسم الله الرحمن الرحیم

الان چیزی که به ذهن من میرسه اینه که اگر توی تعریف دور، تکراری نبودن رئوی مد نظر باشد، حکمی که در سؤال آمده صحیح نیست.

مثال:

$n$ رو قرار بدید $3$ و گراف جهتدار زیر را در نظر بگیرید :

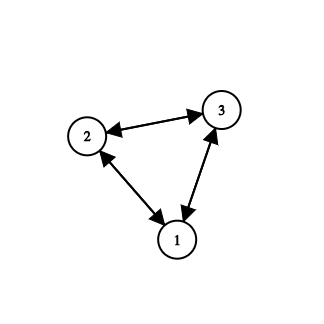
الان این گراف، شرایط گفته شده در صورت سؤال رو داره، اما حکم برای آن درست نیست.

یا حتی اگر دوست داشته باشید که بین هر دو رأس از گراف حداکثر یک یال موجود باشد، میتوانید مثال زیر را برای $n=5$ ببینید:

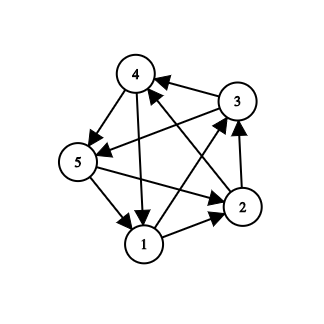
با یه مقدار حوصله میشه دید که حکم برای این گراف هم صحیح نیست.

و با یک مقدار حوصله بیشتر میشه دید که برای هر $n$ دلخواه، یک گرافی با شرایط گفته شده وجود داره که ، حکم براش صحیح نباشه.(چرا؟)

اما اگر شرط تکرای نبودن رئوس را نداشته باشیم، یعنی بخواهیم به جای دور، بخواهیم گذر بسته پیدا کنیم، میتوانیم حکم رو اینجوری اثبات کنیم:

یک گراف دوبخشی در نظر بگیرید که هر بخش دارای $n$ رأس با شماره‌های $1$ تا $n$ هست.

در این گراف دو بخشی یال $i$ از بخش اول را به یال $j$ از بخش دوم وصل میکنیم اگر و تنها اگر در گراف اصلی یک یال جهتدار از $i$ به $j$ داشته باشیم. مثلا برای گراف بالا، گراف دو بخشی اون رو اگه بکشیم، این شکلی میشه :

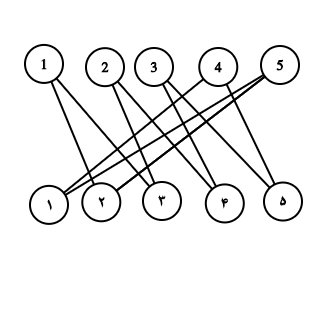
حالا یک گراف دوبخشی با مجموع $2n$ رأس و بیشتر از $2n$ یال داریم. پس قطعاً این گراف درخت نیست و دور دارد.

با یه مقدار تلاش میشه فهمید که این دوری که در این گراف دوبخشی پیدا کردیم، بهمون یک گذر بسته میده توی گراف اولیه که جهت یالها در آن یکی در میان است.