تعاریف:

زوج زشت: در جایگشت $p$ از اعداد 1 تا $n$ به زوج $(p_i,p_{i+1})$ ($i \le n-1$) زشت میگوییم اگر و تنها اگر: $|p_i-p_{i+1}=1|$

جایگشت زشت: به جایگشتی از اعداد 1 تا $n$ که شامل زوج زشت $(n,n-1)$ یا $(n-1,n)$ باشد زشت میگوییم.

جایگشت زیبا: به جایگشتی که زشت نباشد زیبا میگوییم.

$a_{i,j,0}$ $(0 \le j \le i-1)$ : تعداد جایگشت های زیبا از اعداد 1 تا $i$ به طوری که $j$ زوج زشت داشته باشد.

$a_{i,j,1}$ $(0 \le j \le i-1)$ : تعداد جایگشت های زشت از اعداد 1 تا $i$ به طوری که $j$ زوج زشت داشته باشد.

راه حل:

میخواهیم به صورت بازگشتی $a_{9,0,0}$ که جواب نهایی ما است بدست بیاوریم. برای اینکار سعی میکنیم با حالت بندی زیر مقدار $a_{i,j,1}$ و $a_{i,j,0}$ $(0 \le j \le i-1)$ را بصورت بازگشتی بدست آوریم. برای اینکار همه ی جایگشت های 1 تا $i-1$ را در نظر میگیریم و تمام حالات قرار دادن $i$ در بین اعضای این جایگشت را بررسی میکنیم.

(این را میدانیم که اگر یک جایگشت از اعداد 1 تا $n$ داشته باشیم با اضافه کردن $n+1$ در هر جایگشت تعداد زوج های زشت حداکثر یکی تغییر میکند.و همچنین درصورت تعریف نشدن یکی از متغیر ها آن را در نظر نمیگیریم. نکته ی دیگری که باید اضافه کنم این است که ما میخواهیم جایگشت اعداد 1تا $i$ به ازای $j$ جفت زشت را بدست بیاوریم پس بنابر این اگر مثلا بخواهیم یک جفت به جفت های زشتمان اضافه شود جایگشت اعداد 1 تا $i-1$ مان باید $j-1$ جفت زشت داشته باشد. به همین صورت برای بقیه ی حالات نیز در نظر بگیرید)

1. تعداد زوج های زشت با اضافه کردن عدد i به جایگشت اعداد 1 تا $i-1$ یک عدد افزایش یابد:

   1.1: جایگشت اعداد 1 تا $i$ زیبا باشد: این حالت امکان پذیر نیست چون برای اینکه عدد $i$ باعث افزایش زوج های زشت شود باید کنار عدد $i-1$ قرار بگیرد که در این صورت جایگشتمان زشت میشود.

   2.1: جایگشت اعداد 1 تا $i$ زشت باشد: در اینصورت اگر جایگشت اعداد 1 تا $i-1$ زیبا باشد 2 مکان برای قرار دادن $i$ داریم(قبل از $i-1$ و بعد از $i-1$ ) اگر هم زشت باشد تنها یک مکان برای قرار دادن $i$ داریم; به این دلیل که در کنار $i-1$ عدد $i-2$ وجود دارد و اگر ما $i$ را بین $i-1$ و $i-2$ قرار دهیم تعداد زوج های زشت تغییر نمیکند. پس فقط یکطرف $i-1$ قادریم $i$ را قرار دهیم. پس بر این اساس باید مقدار$a_{i-1,j-1,0} \times 2 + a_{i-1,j-1,1}$ به $a_{i,j,1}$ اضافه شود.

2. تعداد زوج های زشت با اضافه کردن عدد i به جایگشت اعداد 1 تا $i-1$ تغییر نکند:

   1.2. جایگشت اعداد 1 تا $i$ زیبا باشد: در این صورت اگر جایگشت اعداد 1 تا $i-1$ زیبا باشد $i-j-2$ حالت برای قرار دادن عدد $i$ داریم. به این دلیل که عدد $i$ را نباید بین دو عدد که با هم تشکیل زوج زشت دارند قرار دهیم چون در این صورت تعداد زوج های زشت کم میشود و همچنین حق نداریم عدد $i$ را در کنار $i-1$ قرار دهیم. پس $i-j-2$ حالت داریم (دقت کنید ممکن از $i-j-2$ منفی شود که در این صورت آن را صفر در نظر میگیریم). اگر هم جایگشت اعداد 1 تا $i-1$ زشت باشد آنگاه $i-j-1 $ حالت داریم. چون علاوه بر حالات ذکر شده در چند سطر قبل میتوانیم $i$ را بین $i-1$ و $i-2$ قرار دهیم (یک زوج زشت از بین رفته و زوج زشت دیگری بوجود می آید) پس در نهایت باید مقدار $a_{i-1,j,0} \times (i-j-2) + a_{i-1,j,1} \times (i-j-1)$ به $a_{i,j,0}$ اضافه شود.

   2.2. جایگشت اعداد 1 تا $i$ زشت باشد: در اینصورت باید $i$ را کنار $i-1$ قرار دهیم و برای اینکه تعداد زوج های زشت تغییر نکند باید جایگشت اعداد 1 تا $i-1$ زشت باشد تا بتوانیم $i$ را بین $i-1$ و $i-2 $ قرار دهیم. (یک زوج زشت کم و یکی اضافه شود). پس یک حالت وجود دارد و در نتیجه مقدار $a_{i-1,j,1}$ باید به $a_{i,j,1}$ اضافه شود.

3. تعداد زوج های زشت با اضافه کردن عدد i به جایگشت اعداد 1 تا $i-1$ یک عدد کاهش یابد:

   1.3. جایگشت اعداد 1 تا $i$ زیبا باشد: در این صورت اگر جایگشت اعداد از 1 تا $i-1$ زیبا باشد $j+1$ جا برای قرار دادن $i$ داریم (بین اعداد $j-1$ زوج زشت) و اگر جایگشت اعداد از 1 تا $i-1$ زشت باشد $j$ حالت داریم. چون $i$ را نمیتوانیم بین $i-1$ و $i-2$ قرار دهیم. پس باید مقدار $a_{i-1,j+1,0} \times (j+1) + a_{i-1,j+1,1} \times j$ به $a_{i,j,0}$ اضافه شود.

   2.3. جایگشت اعداد 1 تا $i$ زشت باشد: این حالت ممکن نیست چون اگر بخواهیم زشت باشد باید $i$ را کنای $i-1$ قرار دهیم پس نهایتا این است که تعداد زوج های زشت تغییری نمیکند و به هیچ وجه کم نمیشود.

حال دو نتیجه ی زیر را میگیریم:

$a_{i,j,0}=a_{i-1,j,0} \times (i-j-2) + a_{i-1,j,1} \times (i-j-1) + a_{i-1,j+1,0} \times (j+1) + a_{i-1,j+1,1} \times j$

$a_{i,j,1}=a_{i-1,j-1,0} \times 2 + a_{i-1,j-1,1} + a_{i-1,j,1}$

تکرار میکنم درصورت تعریف نشدن یکی از متغیر ها آن را در نظر نمیگیریم.

در جدول زیر مقادیر را نوشته ایم: (سطر ها نشن دهنده ی $i$ ستون ها $j$ و مکان هایی که INVALID نوشته شده نیازی به بدست آوردنشان نداریم و به ما کمک نمیکند و یا اینکه تعریف نشده اند. همچنین اعداد اول هر خانه مقدار جواب به ازای جایگشت زیبا و بعدی به ازای جایگشت زشت است):

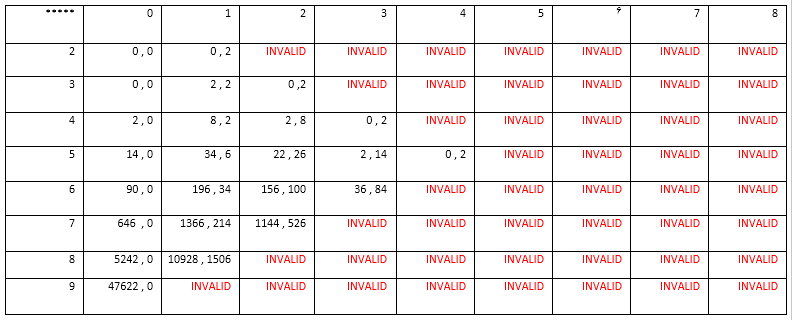
با توجه به جدول جواب آخر 47622 است.