عکسا رو تو یه سایتی آپلود کردم که لیمیت نداشته باشه 🗿
بدون عکس کل اثباتم به فنا می رفت...
2024-03-02 08:40:14 -0500 سیده زینب متولیاولین باره که به کاهو میای؟ راهنمای سایت رو حتما بخون!
سوال ۱ روز دوم مرحله ۲ دوره ۲۳: رشتهی نزدیک
بازی رنگی - سوال ۱ - مرحله ۲ - ۱۳۹۳
وزنهها و ماشین جادویی - سوال ۲ - مرحله ۲ - ۱۳۹۳
گاوی خسیس - سوال ۳ - مرحله ۲ - ۱۳۹۳
انتقال مهرههای گاوی - سوال ۴ - مرحله ۲ - ۱۳۹۳
یافتن کوچکترین پیچ و مهره با مقایسه آنها
دنباله و جادوگر - دوره ی 24 - مرحله ی 2
مسئله ی مسیر و شبکه - مرحله ی 2 – دوره ی 23
در این قسمت میتونی به یک پرسش پاسخ بدی. اگه میخوای در مورد پرسش بحث و اظهار نظر کنی از قسمت «ثبت نظر» استفاده کن.
پاسخت رو دقیق و کامل بنویس، از عکس استفاده کن و اگه لازمه به منابع (کتاب یا سایت) ارجاع بده.
اگه پرسش یا پاسخها مفید هستند حتما بهشون رای بده تا پرسشها و پاسخهای خوب مشخص بشن.
توی قسمت پیشنمایش میتونی ببینی متنی که نوشتی چجوری روی سایت دیده میشه.
خیلی مهم: برای اینکه به خط بعد بری باید دوتا Enter بزنی.
میتونی از تگهای معمولی و سادهی html هم استفاده کنی.
با دکمههایی که بالای ویرایشگر قرار دارند کلی کار میشه کرد. از عکسگذاشتن بگیر تا لیست شمارهدار. حتما امتحانشون کن.
برای نوشتن علائم ریاضی میتونی از Mathjax استفاده کنی.
راهنمای Mathjax رو از سایت
math.stackexchange
بخون.
برای نوشتن عبارت ریاضی وسط جمله، اون عبارت رو بین دوتا $ قرار بده.
برای نوشتن عبارت ریاضی تو یه خط جدید اون رو بین دوتا $$ قرار بده.
زاریچ که زندگی خود را وقف شکست ویروس کرونا کرده است، یک ربات برای ضدعفونی کردن زمین اتاق ساخته است. زمین اتاقی که ربات در آن قرار دارد از بالا به صورت جدولی مربعشکل دیده میشود. ربات در ابتدا روی خانهی گوشهی پایین-چپ جدول قرار دارد. در برخی خانههای جدول وسایل قرار دارد و آن خانهها مسدود است. ربات ابتدا رو به بالای جدول قرار دارد و همواره بهصورت زیر حرکت میکند:
اگر ربات مقابل دیوار قرار نداشت و خانهی مقابل ربات مسدود نبود، ربات یک خانه به جلو حرکت میکند. در غیر این صورت، ربات ۹۰ درجه در جهت ساعتگرد میچرخد. این ربات در حین حرکت، روی هر خانهای از جدول که برود، آن را ضدعفونی میکند. هدف زاریچ آن است که همهی خانههای قطر اصلی جدول حداقل یک بار توسط ربات پیموده و ضدعفونی شوند. قطر اصلی مجموعهای از خانههای جدول است که از خانهی بالا-چپ جدول شروع میشود و تا خانهی پایین-راست جدول ادامه مییابد. امکان دستیابی به هدف زاریچ به این بستگی دارد که چه خانههایی از جدول مسدود باشند. اگر در یک جدول، ربات (با شروع از خانهی پایین-چپ و جهت اولیهی رو به بالا، و حرکت طبق قواعد گفته شده) همهی خانههای قطر اصلی را حداقل یک بار ضدعفونی کند، آن جدول را مطلوب مینامیم. بالطبع، هیچ یک از خانههای قطر اصلی و یا خانهی شروع ربات در یک جدول مطلوب مسدود نیست. مثلا در شکل زیر، یک نمونه از جدول 5×5 را میبینیم که مطلوب نیست. در این جدول، خانههای قطر اصلی با دایره، خانههای مسدود با رنگ سیاه، و خانههای ضدعفونیشده با رنگ خاکستری مشخص شدهاند. همانطور که مشخص است، در این جدول ربات تنها ۲ خانه از ۵ خانهی قطر اصلی را ضدعفونی میکند.
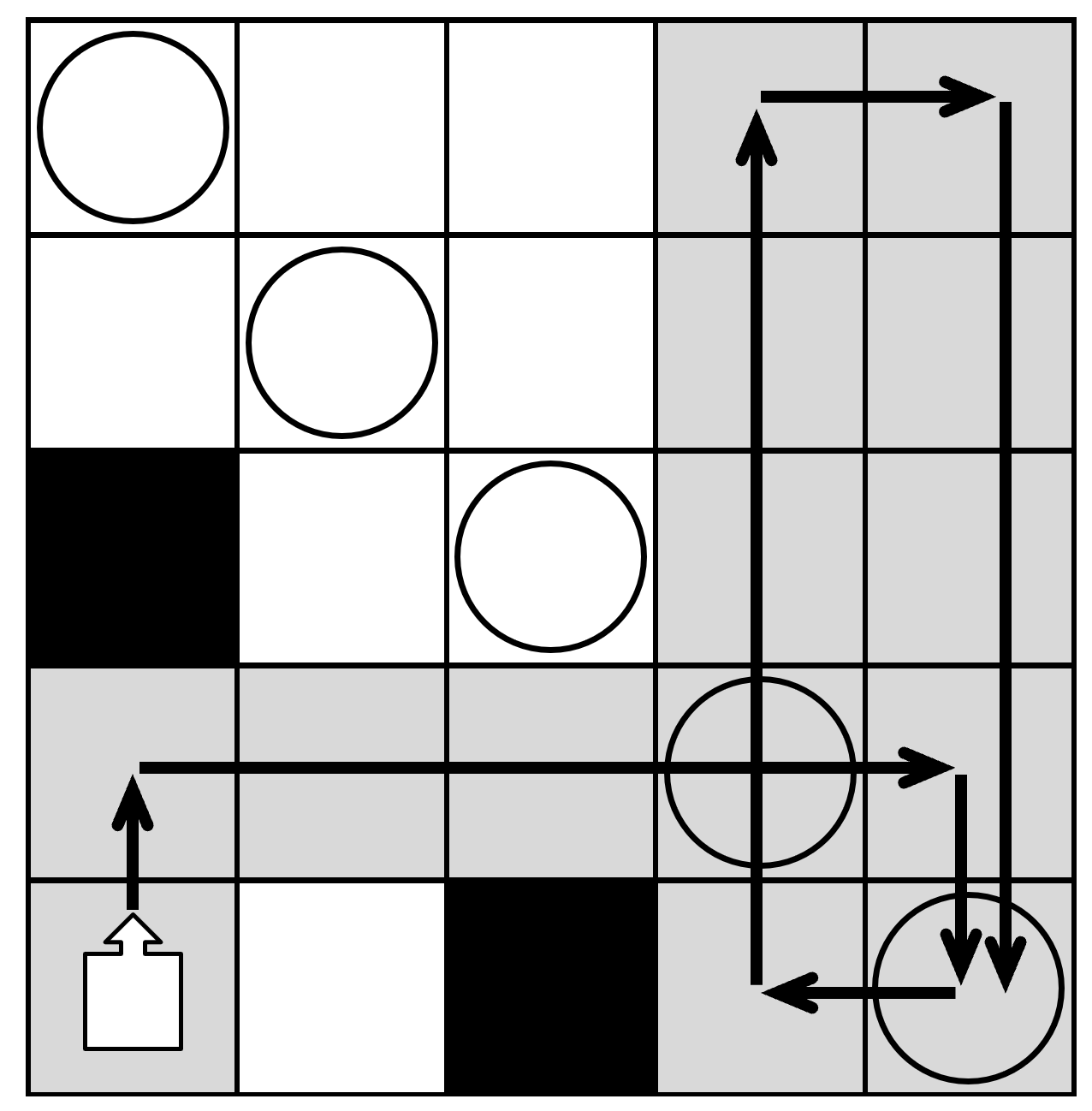
الف) یک نمونه جدول مطلوب 5×5 بکشید. (۵ نمره)
ب) آیا جدول مطلوب ۱۳۹۹×۱۳۹۹ داریم؟ در صورت وجود، آن را توصیف کنید، و در غیر این صورت، ثابت کنید که وجود ندارد. (۱۵ نمره)
برای قسمت الف، به صورت زیر است:
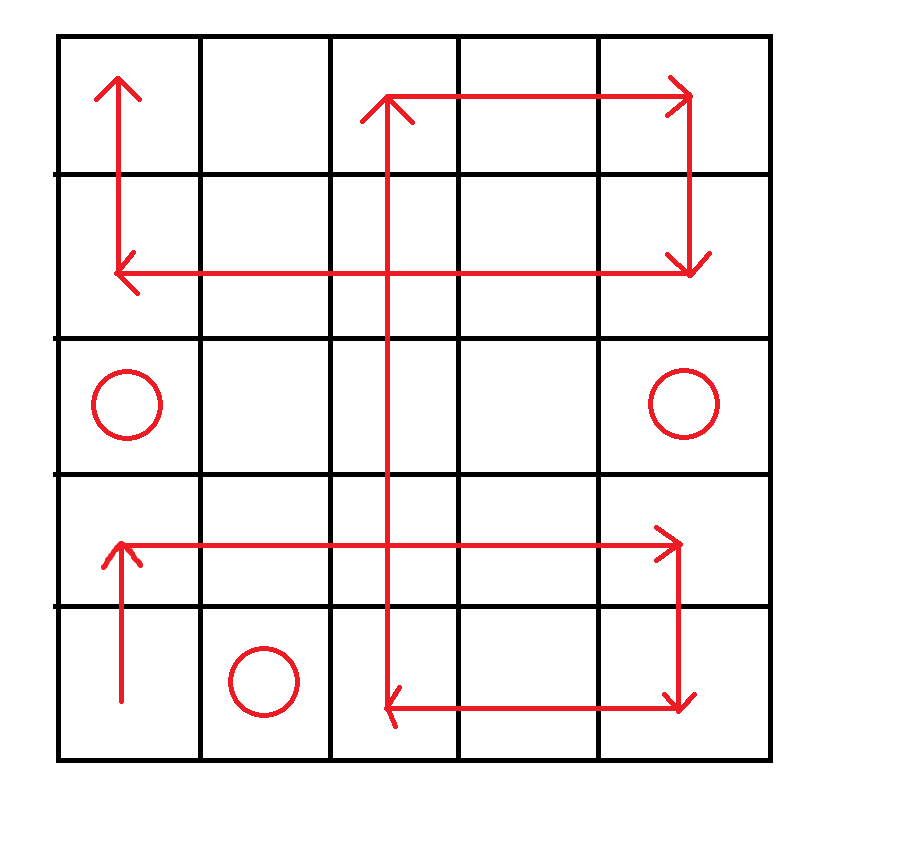
حالا برا قسمت ب هم اثبات می کنم که به ازای n های فرد (n>=5) جدول مطلوب n*n ای با خواص زیر وجود دارد:
از گوشه ی بالا چپ، دقیقا یک بار عبور کنیم و همچنین، آخرین خانه ای باشد که از آن عبور می کنیم و از خانه پایینی اش واردش شده باشیم.
پایه ی استقرا، n=5 هست (می تونید چک کنید که تمام خواصی که ذکر کردم در تصویر جدول 5*5 برقراره).
فرض استقرا: حکم برای n صحیح است (یعنی جدول مطلوب n*n با خواص که ذکر کردم وجود دارد).
شکل زیر، تصویر شکلی هست که توضیحات اثباتم رو با کمکش بیان می کنم؛ پس حتما با توجه به شکل، توضیحاتم رو بخونید:
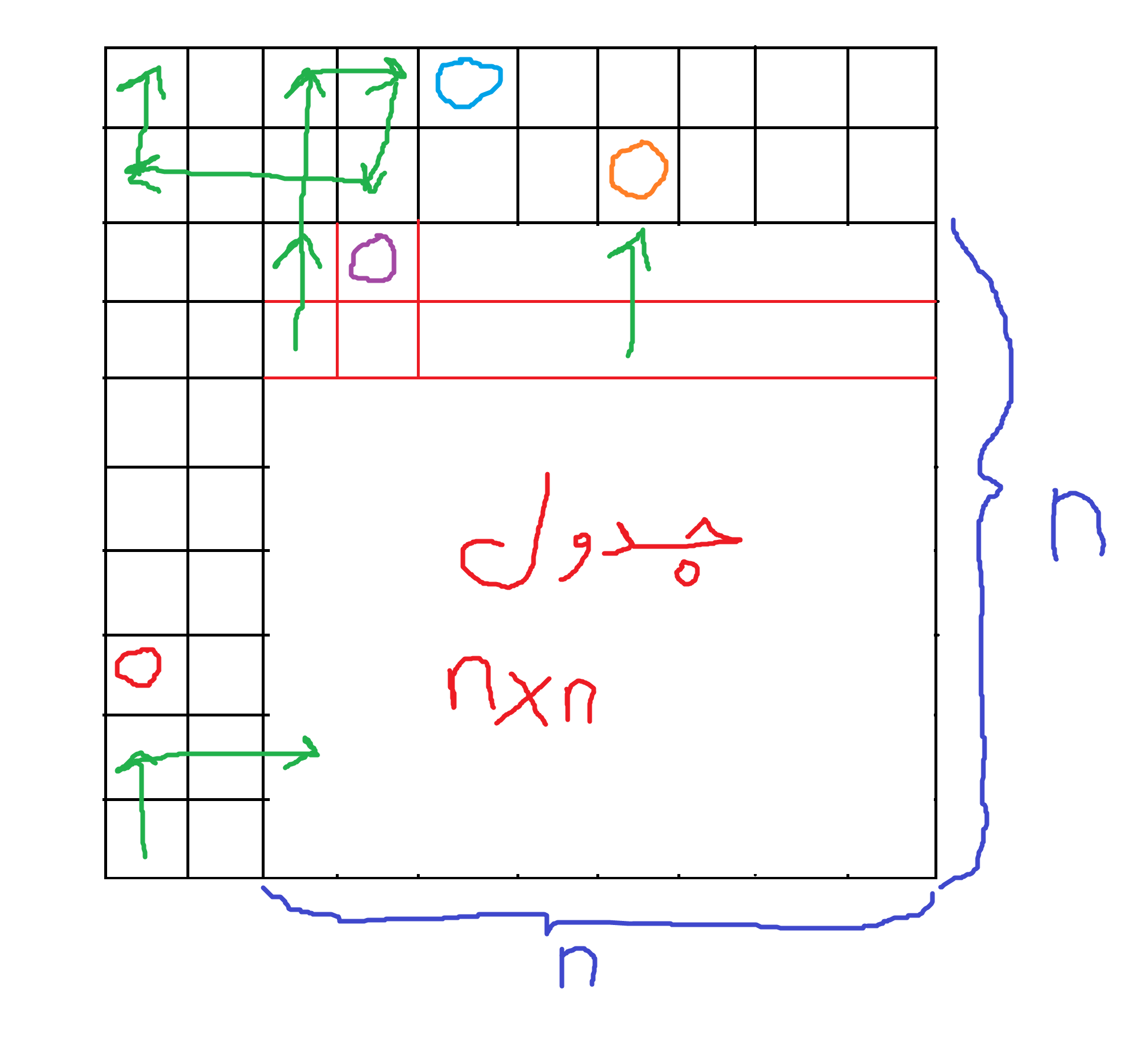
در ابتدای حرکت، ما از خونه ی پایین چپ شروع می کنیم و دو واحد به سمت بالا می یایم. حالا مانع قرمز رنگ باعث می شه که به سمت راست چرخش کنیم و وارد محدوده ی جدول n * n می شیم. حالا از اینجا به بعد رو طبق فرض استقرا می تونیم انجام بدیم طوری که خانه های قطری که در این محدوده هستن رو ببینیم. فقط نکته ای که وجود داره اینه که اگه درجایی از حرکاتمون به ضلع قسمت بالای محدوده ی جدول n * n رسیدیم، یک مانع در خانه ی بالایی آن قرار می دهیم تا حرکاتمان طبق فرض استقرا پیش برود (مانند مانع نارنجی رنگ). می دانیم که پایان حرکاتمان در محدوده ی جدول n * n، در گوشه ی بالا چپ است که طبق فرض، ما از خانه ی پایینی اش وارد آن شدیم (پس منطقا جهت حرکت به سمت بالا بوده). حالا با توجه به شکل، از محدوده ی جدول n * n خارج می شویم و مانند شکل پیش می رویم تا به مانع آبی رنگ برخورد کنیم. می دانیم طبق فرض استقرا، از خانه ای که در آن مانع بنفش قرار گرفته هیچگاه عبور نکرده ایم و به همین دلیل، مانع بنفش را در آن قرار می دهیم. بقیه ی حرکات رو هم با توجه به شکل پیش می ریم. خیلی راحت می تونید چک کنید که جدول مطلوب هست و تمام خواصی هم که درحکم استقرا بیان نمودم، در اینجا هم برقرار است. پس حکم به ازای n+2 نیز درست است.
عکسا رو تو یه سایتی آپلود کردم که لیمیت نداشته باشه 🗿
بدون عکس کل اثباتم به فنا می رفت...
2024-03-02 08:40:14 -0500 سیده زینب متولیبنظر من جواب میتواند باشد![image description]
یاعـــــــــــــــــــــــــــــــــــــــــــــــــــــــلی
کاش این 100 کاراکتر مجاز رو بردارید
توی عکس گفتم دیگه
دوستان چطور میتونم عکس به عنوان جواب آپلود کنم نمیشه میگه should karma>5 من که نفهمیدم شما بفرمایید
2021-06-10 07:36:24 -0500 معین یوسفی نیا