من برای n های زوج اثبات کردم که نمیتونه ببره بعد برام یه سوال پیش اومد اگه اینو اثبات کردم چند نمره از سوال رو میگیرم ؟ نصف ؟ ربع ؟ هیچ ؟
2024-03-02 04:42:27 -0500 الفبادقیقا منم، فقط یادم نیس زوج رو اثبات کرده بودم یا فرد رو. اثباتشم با رنگ آمیزی بود. حالا باید دوباره بررسی کنم
2024-03-02 05:47:09 -0500 سیده زینب متولییادمه یه جا خونده بودم که نمره دهی مرحله دو صفر و یکی هس. ینی اگه راه محلمون کامل باشه نمره کامل می گیریم، و اگه ناقص باشه نمره نمی گیریم...
2024-03-02 05:49:07 -0500 سیده زینب متولیخب اگه این طور باشه قطعا خبر بدیه ولی خب اسم رنگ امیزی رو که آوردی راهم کامل شد
2024-03-02 06:08:17 -0500 الفباآره اصن اثبات منم برا n های فرد بوده و رنگ آمیزیم هم شطرنجی (در حالت n های فرد زاریچ استراتژی برد داره)
2024-03-02 08:23:33 -0500 سیده زینب متولی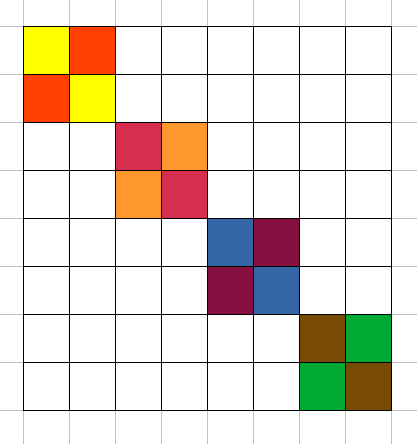 کرونا در هر مرحله باید دو خانه همرنگ از هر مربع را انتخاب کند. واضح است که این
$n$ خانه همیشه یک قطر پراکنده میسازند.
کرونا در هر مرحله باید دو خانه همرنگ از هر مربع را انتخاب کند. واضح است که این
$n$ خانه همیشه یک قطر پراکنده میسازند.