قسمت الف:

نکته 1: تعداد کل مسیرهای یک درخت n راسی، برابر است با ${n \choose 2}$.

نکته 2: تعداد مسیرهای به طول یک در یک درخت n راسی برابر است با n-1.

تعریف: یک مسیر را مزاحم می نامیم اگر A_پسند نباشد .

لم #: تعداد مسیرهای به طول دو یا بیشتر از 1401، در یک درخت 2022 راسی حداقل برابر 2021 است.

اثبات لم: دو حالت کلی برا درخت 2022 راسی در نظر می گیریم:

1. درخت ما یک مسیر به طول 2021 باشد (یعنی درجه ی هر راس حداکثر دو است). در اینصورت تعداد مسیرهای به طول 2 در آن، 2020 است. همچنین طول مسیر بین راس ابتدا و انتهای مسیر نیز 2021 است که از 1401 بیشتر می باشد؛ پس در این حالت حداقل 2021 مسیر مزاحم به طول دو یا بیشتر از 1401 داریم.

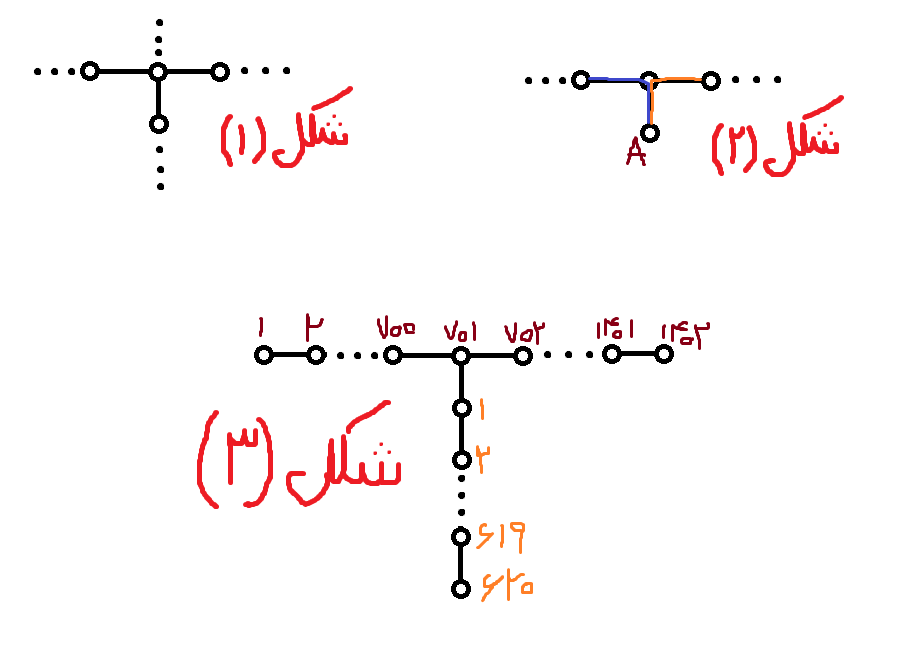
2. درخت ما حداقل یک راس با درجه ی حداقل 3 داشته باشد (شکل 1) . حال فرض کنید که می خواهیم چنین درختی را بسازیم؛ به اینصورت که ابتدا یک مجموعه در نظر می گیریم و داخلش یک راس قرار می دهیم. سپس در 2021 مرحله ی دیگر و در هر مرحله یک راس جدید به مجموعه مان اضافه می کنیم و آن را به یکی از رئوس قبلی مجموعه مان وصل می کنیم (ما حواسمون هست که می خوایم درختمون حداقل یک راس با درجه ی 3 داشته باشه و تضمین می کنم که درخت نهایی مون، حتما چنین ویژگی ای داره). واضح است که بعد از هر مرحله، تمام رئوس داخل مجموعه تشکیل یک درخت می دهند. اولین جایی را در نظر بگیرید که بعد از اضافه کردن یک راس مانند A و متصل کردن آن به یکی از رئوس مجموعه، یک راس با درجه ی حداقل سه داشته باشیم. در اینصورت دو مسیر جدید به طول دو در درختمان ایجاد می شود که یک سر هرکدامشان، راس A است (شکل 2). همچنین، به غیر از اولین و دومین راس، هر راس دیگری را که به مجموعه اضافه می کردیم، حداقل یک مسیر به طول دوی جدید در درختمان پدید می آمد (چرا؟). با این توصیفها، بعد از اضافه کردن تمامی راسها و ساختن درخت 2022 راسی که حداقل یک راس درجه سه دارد، ما حداقل 2021=2+2019 تا مسیر به طول دو داریم.

پس در هر دوحالت بالا، حداقل 2021 مسیر به طول دو یا بیشتر از 1401 داریم؛ حالا درختی ارائه می دهم که دقیقا 2021 مسیر به طول 2 یا بیشتر از 1401 داشته باشد: ابتدا یک مسیر با 1402 راس و یک مسیر با 620 راس می سازم؛ سپس یک سر مسیر 620 راسی را با یک یال به راس 701 ام مسیر 1402 راسی وصل می کنم (شکل 3). خیلی راحت می توانید بررسی کنید که این درخت، هیچ مسیر به طول بیشتر از 1401 ندارد و همچنین، تعداد مسیرهای به طول دو در آن دقیقا برابر 2021 است.

با توجه به نکته 1، نکته 2 و لم # پاسخ قسمت الف برابر است با: 2021-2021-${2022 \choose 2}$

قسمت پ: درختمون باید به شکل زیر باشه و جواب 311*311 هست. از اونجایی که سر نوشتن اثبات قسمت الف خیلی خسته شدم و خب اثبات این قسمت هم یه کمی طولانیه (البته نه به اندازه ی قسمت الف) اثباتشو به خودتون واگذار می کنم