آمار پرسش:
- پرسیده شده: 2024-02-15 05:09:54 -0500
- مشاهده شده: 317 بار
- بروز شده: 2024-02-16 12:16:49 -0500
پرسشهای مشابه:
سوال ۱ روز دوم مرحله ۲ دوره ۲۳: رشتهی نزدیک
بازی رنگی - سوال ۱ - مرحله ۲ - ۱۳۹۳
وزنهها و ماشین جادویی - سوال ۲ - مرحله ۲ - ۱۳۹۳
گاوی خسیس - سوال ۳ - مرحله ۲ - ۱۳۹۳
انتقال مهرههای گاوی - سوال ۴ - مرحله ۲ - ۱۳۹۳
یافتن کوچکترین پیچ و مهره با مقایسه آنها
دنباله و جادوگر - دوره ی 24 - مرحله ی 2
مسئله ی مسیر و شبکه - مرحله ی 2 – دوره ی 23
نکاتی در مورد نوشتن پاسخ:
استفاده از ویرایشگر:
علائم ریاضی:
سوال چهارم: توپ های سیاه و سفید (مرحله2-1402)

.....................
2 پاسخ
قسمت ب واقعا راه جالبی داره.
اولا که زیررشته شامل کل توپ ها متوازنه، پس کافیه ثابت کنیم ۷۰۱ زیررشته متوازن دیگه هم داریم. حالا توپ ها رو دور دایره میچینیم(!). ادعا میکنم به ازای هر k از بین ۱ تا ۱۴۰۱، زیررشته ای از توپ ها (دور دایره) به طول 2k وجود داره که متوازنه. برای اثبات ادعای بالا برای k اینگونه عمل میکنیم: اول روی هر توپ سفید عدد ۱ و هر توپ سیاه -۱ مینویسیم. حالا یه زیررشته دلخواه به طول 2k رو در نظر بگیرید (توجه کنید 2n تا زیررشته دور دایره به طول x وجود داره). اگر جمع اعداد این زیررشته برابر ۰ باشه حله، پس بدون از دست دادن کلیت فرض میکنیم این مجموع کمتر از ۰ باشه. اگر این مجموع رو به ازای تمام 2n حالت انتخاب زیررشته حساب کنیم، با یه دوگانه شماری چون هر توپی در 2k زیررشته حساب میشه و مجموع توپ ها ۰ هست، مجموع ۰ خواهد شد. بنابرین یک زیررشته وجود داره که جمعش مثبته. حالا اگر یک زیررشته رو یک واحد در جهت ساعتگرد شیفت بدیم، با یک بررسی ساده متوجه میشیم که جمعش یا ثابت میمونه یا + یا - ۲ میشه. بنابرین طبق پیوستگیگسسته اگر از زیررشته با جمع منفی هردفعه شیفت بدیم تا به زیررشته با جمع مثبت برسیم، این وسط زیررشته ای وجود داره که جمعش ۰ هست. پس ادعا ثابت شد.
حالا هرعدد مثل k رو میگیم بد اگر زیررشته به طول 2k ای که پیدا کردیم شامل هردوی توپ های 1 , 2n باشه. در غیر این صورت میگیم خوب. اگر تعداد k های خوب بیشتر مساوی ۷۰۱ باشه حکم نتیجه میشه. در غیر این صورت تعداد k های بد حداقل ۷۰۱ = ۷۰۰-۱۴۰۱ هست. حالا فکتی که وجود داره، اینه : اگر یک زیررشته دور دایره جمعش ۰ بشه، جمع زیررشته مکملش هم ۰ عه. یعنی به ازای هر k بد یه زیررشته متوازن در حالت خطی داریم و مجدد حکم نتیجه میشه!
آووو، احسنت. من این دوگانه شماری رو بدون اینکه توپ هارو دور دایره بچینم انجام دادم، برا همین محاسباتم خیلی سخت شد و ولش کردم (چون به ازای هر زیررشته با طول k، تعداد زیررشته هایی که k توپ اول و k توپ آخر در اون اومدن با بقیه نابرابره!)؛ ایده ی چیدن دور دایره خیلی جالب و خفن بود 👌
2024-02-16 13:44:19 -0500 سیده زینب متولیالبته باید این نکته رو هم اضافه کنی که در هر زیررشته به طول 2k، جمع اعداد زیررشته همواره زوجه (دلیلشم اینه که زوجیت 1 ها و 1- ها یکسانه). در واقع اگه بخواد جمع یک زیررشته فرد باشه، اون وقت اون قسمتی که گفتی "طبق پیوستگی گسسته... " اشتباه در می یاد و تو هیچ وقت به جمع صفر نمی رسی.
2024-03-18 22:06:46 -0500 یک عدد انسانحق با شماست. فکر میکردم واضحه و نیاز به اشاره نیست. هرچند در آزمون رسمی باید نوشت این چیز ها رو اما تو کاهو هدف این نیست که خواننده راه حل هم ذهنش درگیر بشه؟
2024-03-20 11:45:26 -0500 فرانسیمتوی راه حل یه مشکلی هست اینکه یه زیررشته ای ممکنه دوره دایره بشمریم ولی اصلا توی زیر رشته ما امکان پذیر
2024-04-03 11:49:12 -0500 امیرعلی جهانیقسمت الف:
چینشی ارائه می دهم که ارزش آن حداکثر 702 است:
به ترتیب از راست به چپ، ابتدا 701 توپ سفید، بعد 1402 توپ سیاه و بعد هم 701 توپ سفید دیگر را قرار می دهیم (مانند شکل زیر)
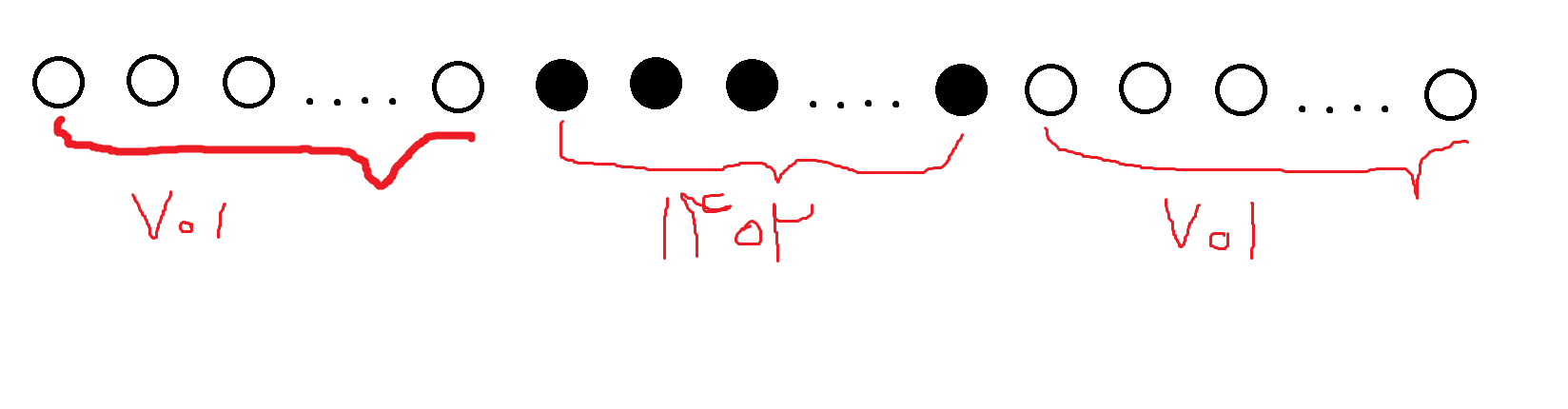
حالا خیلی راحت می تونید بررسی کنید که هیچ رشته ی متوازنی به طول بیشتر از 1402 و کمتر از 2804 در این چینش وجود ندارد. در حقیقت، مجموعه ی طول رشته های متوازن این چینش، زیر مجموعه ای از {1400,1402,2804,...,2,4,6,8} است؛ پس حداکثر 702 عضو دارد (از اونجایی که خیلی واضحه اثباتشو به عهده ی خواننده می ذارم! قسمت مهمش ارائه دادن چینش بود)
پ.ن: می تونید بررسی کنید که مجموعه ی طول زیررشته های متوازن این چینش، شامل تمام عضو های مجموعه ای که ذکر کردم می شه (یعنی ارزش چینش، دقیقا 702 عه!)