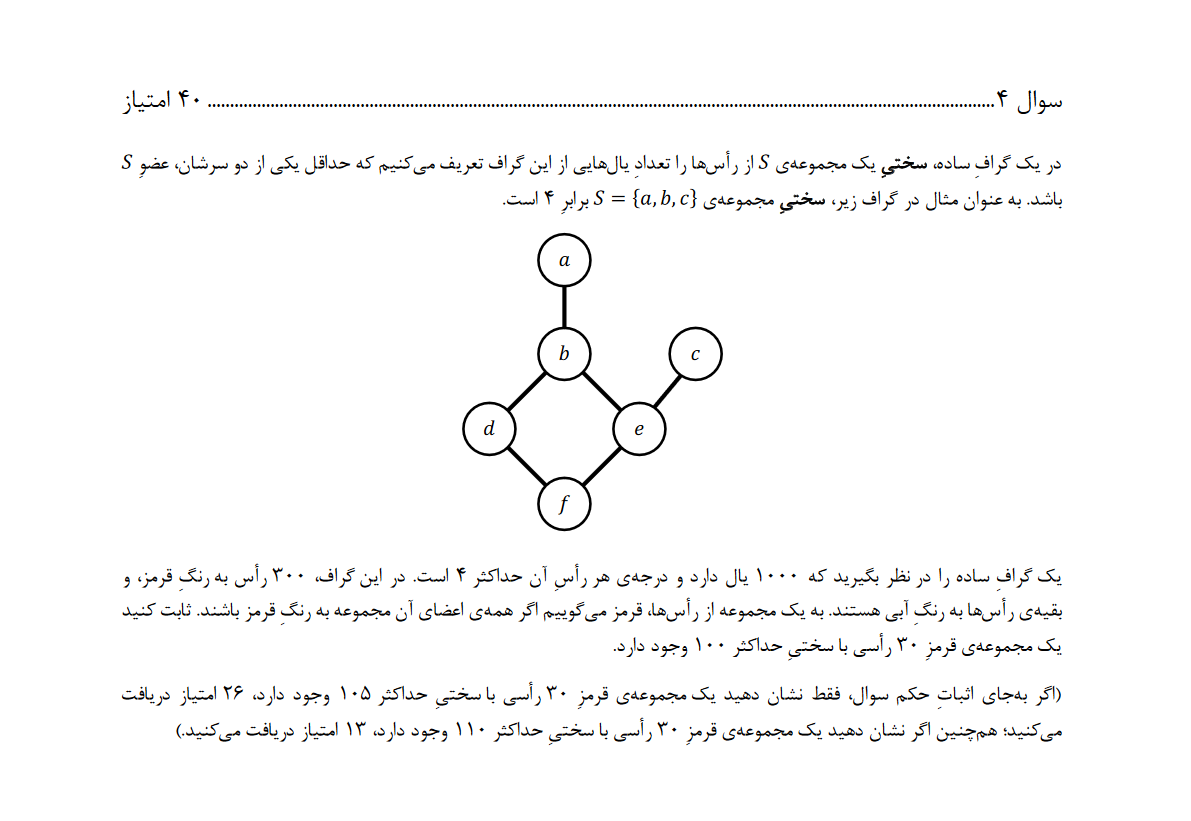
ابتدا رئوس قرمز رو بر اساس درجه‌شون از کوچک به بزرگ مرتب می‌کنم و در یک لیست می‌نویسم. اگه جمع درجات ۳۰ راس اول کوچکتر مساوی ۱۰۰ باشه این ۳۰ راس جوابه. پس درجه راس ۳۱م ( و بقیه رئوس) دقیقا ۴ هست. ( اگر ۳ باشه جمع درجه ۳۰ تای اول حداکثر ۳ * ۳۰ = ۹۰ هست). پس جمع درجات کل رئوس قرمز حداقل ۱۱۸۰ = ۱۰۰ + ۴ * ۲۷۰ هست. یعنی اگه $m$ برابر تعداد یال های دو سر قرمز باشه داریم $$1180 - m \le 1000 => m \ge 180$$

حالا اثبات میکنم یه مجموعه قرمز۳۰ راسی وجود داره که زیرگراف القاییش حداقل ۲۰ یال داره. برای اینکار راس های آبی رو میریزم دور. حالا گراف رو با مولفه های هم‌بندیش در نظر میگیرم و یک لم رو بررسی میکنم.

لم : اگر گراف n راسی همبند باشه، یک راس غیر برشی داره در نتیجه میشه به گراف هم‌بند n-1 راسی رسید. (اثباتش با خودتون)

حالا اگه تعداد مولفه ها کمتر مساوی ۱۰ باشه، یه مولفه با حداقل ۳۰ راس داریم. اونقدر ازش راس کم میکنیم ( طبق لم) که ۳۰ راسی بشه. چون همبنده پس ۲۹ یال داره. پس فرض میکنیم بیشتر از ۱۰ مولفه داریم. ۱۰ مولفه با بیشترین راس را در نظر بگیرید. حالا روی جمع تعداد رئوس این مولفه ها حالت بندی میکنم.‌

۱) بیشتر مساوی ۳۰. باز طبق لم راس حدف میکنیم تا دقیقا ۳۰ راس بشه. چون تعداد یال ها $\le$ تعداد مولفه ها - تعداد رئوس هست پس این ۳۰ راس حداقل ۲۰ یال دارن!

۲) کمتر از ۳۰. پس سایز هر مولفه دیگه ای حداکثر ۲ هست ( اگر ۳ باشه، ۱۰ مولفه اول حدقل ۱۰ * ۳ = ۳۰ راس دارن) یعنی جمع یال های سایر مولفه ها حداکثر ۱۵۰ = ۲ / ۳۰۰ هست یعنی جمع یال های این ۱۰ مولفه حداقل ۳۰ هست. حالا به دل خواه راس برمیداریم تا دقیقا ۳۰ راس داشته باشیم.

پس در نهایت ۳۰ راس داریم که در بینشون حداقل ۲۰ یال هست. پس سختی این مجموعه حداکثر 100 = 20 - 4 * 30 خواهد بود!

پ.ن : دقت کنید جوب نباشه 😂

یک مجموعه قرمز ۳۰ رأسی با سختی حداکثر ۱۰۵ وجود دارد (۲۶ امتیاز)

اگر ۱۵ یال دو سر قرمز داشته باشیم:

رأس‌های دو سر این یال‌ها را در نظر بگیرید. (حداکثر تعدادشون ۳۰ تا است) اگر تعداشون کمتر بود به صورت دلخواه چند رأس قرمز دیگر اضافه کنید تا یک مجموعه ۳۰ تایی قرمز به دست بیاد.

اگر ۱۵ یال دو سر قرمز نداشته باشیم:

تمام یال‌های دوسر قرمز را در نظر می‌گیریم و تمام رأس‌هایی که در دو سر این یال‌ها هستند رو حذف می‌کنیم. ( تعداشون حداکثر ۲۸ است)

حالا از میان بقیه رئوس قرمز، ۳۰ رأسی که کمترین درجه‌ها را دارند را انتخاب می‌کنیم.