میشه جمله ی n ام دنباله اعداد کاتالانی.یعنی$\frac{1}{n+1}\binom{2n}{n}$

من خودم از طریق تناظر با یکی از جواب های دنباله کاتالانی حل میکنم ولی اگه کسی مستقل حلش کنه یعنی رابطه دنباله اعداد کاتالانی رو مستقل اثبات کرده که خودش خیلیه!!

و اما اثبات:

میدونیم تعداد راه های پیمودن یه جدول n*n از روی خطوط از گوشه پایین چپ به گوشه بالا راست طوری که هیچوقت از خط واصل پایین چپ به بالا راست بالاتر نریم جمله n ام دنباله کاتالانیه:

خب فرض کنید n تا سکه در زیر داریم.به ازای هر جواب این مسئله کافیه سکه های رویی رو در نقاطی بچینیم که تو مسیر از اون ها عبور کردیم و نقاط زیر اون ها.(اول شکلو 135 درجه بچرخونید بعد این کارو بکنید واگرنه سکه ها میریزن!!)مثلا:

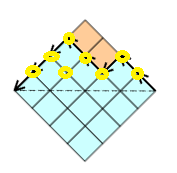
خب واضحه که به هر حالت چیدن سکه ها هم یکی از این مسیر ها متناظر میشه پس تناظر یک به یکه و مسئله حلّه.

موفق باشید!

شکل از:ویکی پدیا

جدای از راه بالایی دنباله بازگشتی سوال رو مینویسیم و میبینیم که ضابطه و پایه اش دقیقا با کاتالان برابره . $A_n$ رو میگیریم جواب. حالت بندی میکنیم روی اولین سکه ای که در طبقه ی دوم نیامده (اینکه تمام n-1 سکه ی طبقه دوم هم آمده باشد حساب میکنیم) .

فرض کنید سکه ی $i$ ام از سمت راست نیامده . ($1 <= i <= n$). پس تمام سکه های سمت راست $i$ در طبقه ی دوم باید آمده باشند پس $A_{i-1}$ برای سکه های سمت راست i در طبقه ی دوم. در مورد سکه های سمت چپ هم میدانیم که آزاد هستیم و میتواند در طبقه ی دوم خالی داشته باشد . پس $A_{n-i}$

در کل : $A_n = \sum_{i=۱}^n A_{i-1} \times A_{n-i}$

و

$A_1 = 1 , A_2 = 2$