فرض خلف میزنیم میگیم که اینجوری نباشه یعنی همه مربع ها 0 تا 2 تا یا 4 تا دارن

خوب بعدش جدول رو به 100 در 100 تا از مربع های دو در دو تقسیم میکنیم با حل معادلات میفهمیم که حداقل 101 تا از مربع ها 4 تا یی (سفید یا سیاه) است

خوب توی هر سطری(سطر هایی از مربع های دو دو یی) اگه یه مربع 4 تایی (سفید یا سیاه)داشته باشیم در این صورت مربع هایی دو دویی اون سطر که 2 تا سیاه دارن (چون باید فرد نباشه مربع 2*2 هایی بینشون )

باید به این شکل

*+

*+

یا

+*

+*

و در ستون

++

11

یا

11

++

باشن خوب چون ما حد اقل 101 تا مربع 4 تا سیاه و 4 تا سفید داریم پس حداقل دو تا مربع چارتایی در سطر و ستون های مختلف وجود داره (لانه کبوتری)که این تناقض ایجاد میکنه

چون مربع دودویی هاشون یکیشون باید

از طرفی

++

11

یا

11

++

و از طرفی

*+

*+

یا

+*

+*

اینجوری باشن که تناقض داره(حواستون باشه که تعداد سیاه ها بر 4 بخش پذیر نیست پس حتما یه دو 2 تا یی داریم)

ویرایش :

معادلات 1 (اول پیدا کردن تعداد سیاه ها و سفید ها):

s+b=40000 s-b=404

s=20202 b=19798

معادلات 2 (پیدا کردن مربعات 2*2 )

0 تا سیاه را m

2تا سیاه را n

4 تا سیاه را o

m+n+o=10000(تعداد مربع هایی که ساختیم)

2n+4o=20202(تعداد سیاه ها)

2n+4m=19798 (تعداد سفید ها)

نتیجه میگیریم که تعداد o+m ها بیشتر از 101 هست

ویرایش 2-

تقسیم به مربع های دو در دو اینجوریه

|++|++|

|++|++|

|++|++|

|++|++|

تداخلی هم که من میگم مثلا منظورم اینه:

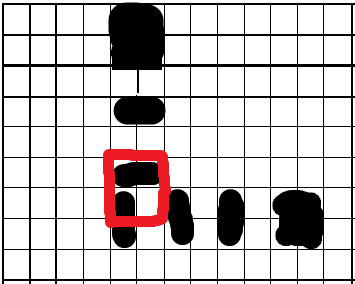
اگه جدول ما چنین مربعی نباشه هر هر دو سطری که متوالی باشند یا با هم مساوی اند یا اگر خانه ای سیاه باشه پایینیش سفیده و برعکس(بدیهیه)
تعداد سیاه ها تو سطر اول رو x در نظر میگیریم و تعداد بار هایی که این سطر تکرار شده رو y در نظر میگریم راستی تعداد سیاه ها هم برابره 20202 هستش پس

20202 = xy + (200-x)(200-y)

20202 = 40000 - 200(x+y) که دو طرف تساوی نمیتونند مساوی باشند ... (بخش پذیری )