آمار پرسش:
- پرسیده شده: 2015-03-04 12:50:54 -0500
- مشاهده شده: 397 بار
- بروز شده: 2015-06-23 20:49:34 -0500
پرسشهای مشابه:
$n$ دایره با شعاع 1 در صفحه حداقل یکدیگر را درچند نقطه قطع میکنند؟
نشان دهید یک مربع به ضلع واحد را نمی توان با 5 مربع با ضلع کمتر از $1/2$ پوشاند .
آشپزباشی: مرتب کردن پشته با برعکس کردن یک دنباله متوالی از ابتدای آن
تعداد جواب های معادله ${1\over x}+{1\over y}={1\over n}$ در دستگاه اعداد صحیح
همه را با تلفن خبر کنید - دوره ی 05 - مرحله ی 1
یکی کردن علامت خانههای یک جدول $4\times 4$ از + و - ها
تبدیل جدول با چرخشهای ساعتگرد مربع $2\times 2$
دو زیرمجموعه فرد و زوج از مجموعه {۱، 2، 3، ...64}
نکاتی در مورد نوشتن پاسخ:
استفاده از ویرایشگر:
علائم ریاضی:
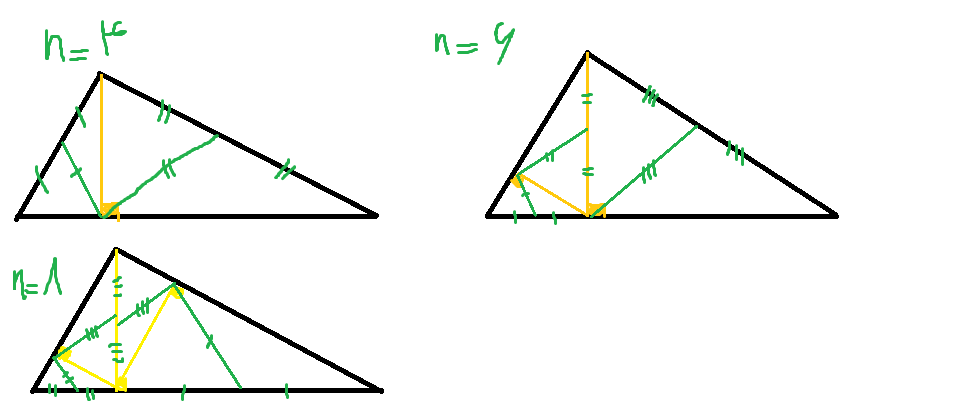
ثابت کنید می توان هر مثلث دلخواهی را به 1386 مثلث متساوی الساقین افراز کرد.
ثابت کنید می توان هر مثلث دلخواهی را به 1386 مثلث متساوی الساقین افراز کرد.
........................
2 پاسخ
سلام.
با استقرا روی تعداد مثلث های ایجاد شده ثابت می کنیم:
اول پایه میزنیم.(پایه هاش رو نمیدونم! خودتون پیدا کنید. D: )
بعد فرض می کنیم که برای n درسته.
حالا ثابت می کنیم برای n+3 درسته.
ما یه مثلث متساوی الساقین انتخاب می کنیم و اوساط اضلاعش رو به هم وصل می کنیم. چهار مثلث متشابه بوجود میاد که
متساوی الساقسن هستند.
یعنی تعداد مثلث ها سه تا افزایش یافته و برای n+3 اثبات شد. ■
روش دوم(شاید هم بهتر)
{
اگه از مرکز دایره ی محیطی به رئوس وصل کنیم برای n+2 حل میشه. در ضمن خودش پایه برای n=3 هم هست.
2015 هم (آره عدد مساله رو تغییر دادم!) در شرایط صدق می کند. ■
}
پرسش جالبی بود که قدرت ترکیبیات رو نشون میده. ترکیبیات برای مسائل هندسی... (;
2015-03-08 11:51:09 -0500 سی پلاس پلاسبابا این همه کارو من کردم! یکیشم خودتون انجام بدید دیگه!!! D:
2015-03-08 11:56:05 -0500 سی پلاس پلاسبرای n-> n+2 ، یه مشکل هست اونم اینه که شاید مرکز دایره محیطی تو مثلث نیفته
2015-03-08 12:13:11 -0500 مجتبی شاهبازیمشکل پایه است.درواقع اینجوری تو فقط داری مثلث های متساوی الساقین رو به مثلث های جدید تبدیل میکنی و تنها مسئله رو برای مثلث ها ی متساوی الساقین اثبات میکنی.
2015-03-08 12:33:11 -0500 روبیک