پیدا کردن مولفه های قویا همبند گراف جهت دار
یافتن کوتاه ترین دور در گراف ساده
جزوه ی برنامه نویسی قسمت (گراف)
پيدا كردن دومين كوتاهترين مسير بين دو راس گراف با توجه به الگوريتم ديكسترا
پیدا کردن گراف دوبخشی کامل یکرنگ
حداکثر تعداد یال‌های گراف بدون مثلث
یافتن کوچکترین پیچ و مهره با مقایسه آنها
100 نفر توی یک اتاق هستن. روی سر هر کس یه کلاه هست که روی اون یک عدد بین 1 تا 100 نوشته شده. هیچکس کلاه خودش رو نمی بینه، ولی شماره ی همه ی کلاه های دیگه رو می بینه. هر کس هم یه برگه داره که باید یه شماره بین 1 تا 100 روش بنویسه. هدف اینه که الگوریتمی داده بشه که به ازای همه ی حالت های شماره های کلاه ها، حداقل 1 نفر تو اون جمع، شماره ی کلاه خودش رو بنویسه. به نکات زیر توجه کنید:
1- طبیعتا این افراد می تونن قبل از رفتن به اتاق و گذاشته شدن کلاه ها روی سرشون با هم هماهنگ کنن و به یه الگوریتم عمل کنن!
2- افراد با هم هیچ ارتباطی ندارن، یعنی نمی تونن با هم حرف بزنن یا علامت بدن، همین طور هیچکس نمی تونه ببینه که بقیه چی می نویسن یا کی شروع به نوشتن می کنن. تنها اطلاعی که از هم دارن، شماره کلاه های همدیگه هستش.
حالا شما یه الگوریتم بدید که حداقل یه نفر شماره کلاه خودشو بنویسه!
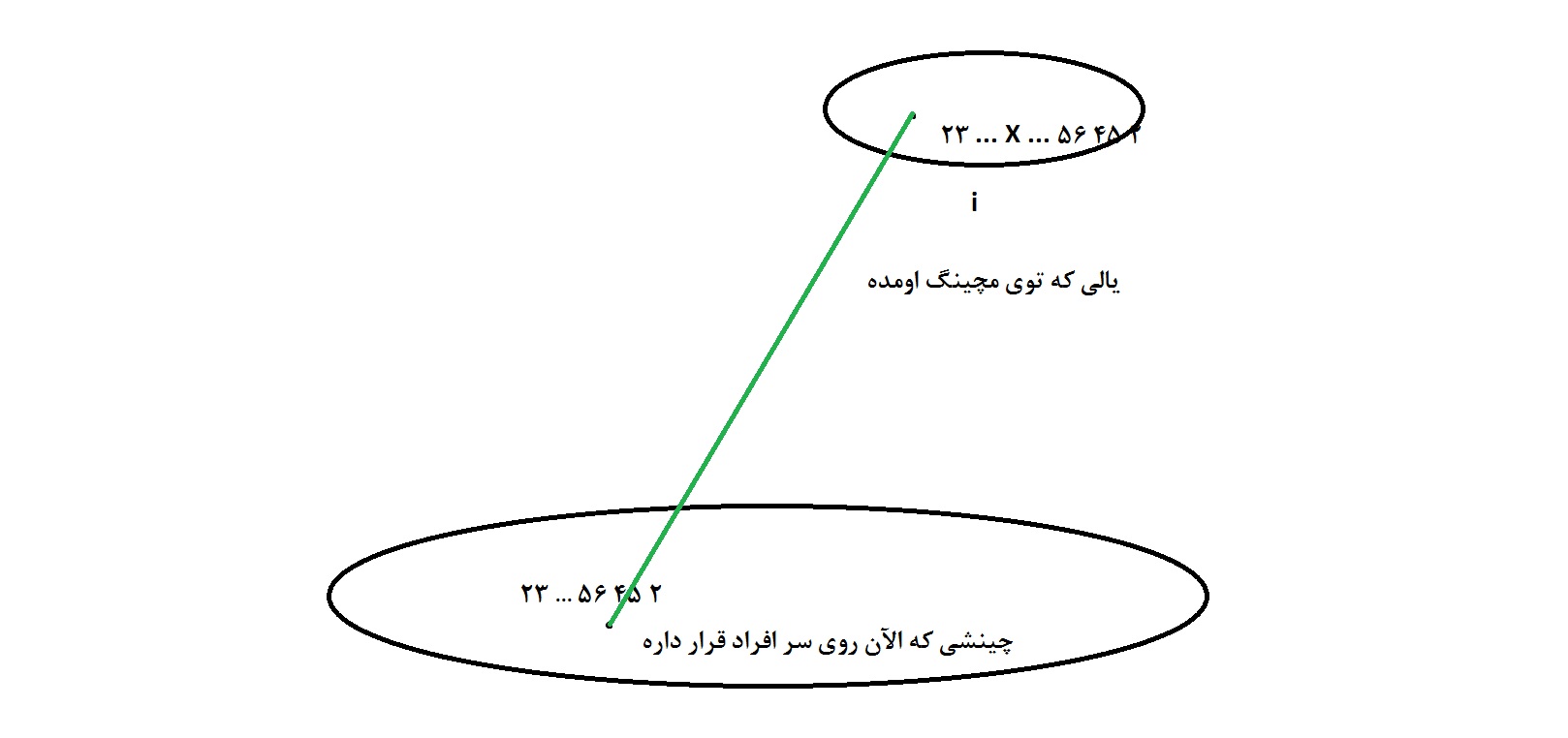
آیا میشه یک عدد تکرار شده باشه؟ یعنی دو نفر کلاهی با شماره 50 داشته باشند؟؟
2015-04-05 10:47:23 -0600 اسپاکسلام میدونستید انجمن علمی نخبگان دانشگاه صنعتی شریف مسابقه تخصصی مهارت سنجی برنامه نویسی و داده کاوی گذاشته است آدرس سایتش www.fanavard.com
2015-08-06 06:45:08 -0600 امیر شکریسلام میگم یک سر به سایت www.fanavard.ir بزنید. مسابقات برنامه نویسی شون شروع شده. گواهی رسمی از طرف دانشگاه شریف می ده. 50 تا سکه هم جایزشه
2016-10-26 10:28:25 -0600 امیر شکریکوتاه می گم قبل از اینکه شروع کنن زندانی ها به خودشون شماره های 1 تا 100 رو می دن حالا اگه نوبت زندانی i باشد فرض می کنه که جمع شماره همه کلاه ها به پیمانه 100 i می شه . و شماره کلاه خودشو حدس می زنه در اخر بالاخره یکی درست می گه!!!
کجاشو نمیفهمی :|| نفر i فرض میکنه که جمع همه کلاه ها باقیماندش به 100 میشه i و با توجه به اون جواب میده
2015-04-07 11:28:05 -0600 حمیدرضاهدرسته! ;) یه راه گراف هم داره، اگه کسی تونست بگه، اگر هم نه خودم بعد چند روز می گم.
2015-04-08 09:52:31 -0600 علی نوروزیاینم راه گراف برای سوال:
ما یه گراف دو بخشی به صورت زیر درست می کنیم: بالا ${100}^{100}$ راس که در 100 دسته ی ${100}^{99}$ تایی دسته بندی شدن، که راس های دسته ی i (در پایه 0)، نمایانگر حالت هایی هستن که راس با اندیس i می تونه از بقیه ببینه. به جای عدد روی کلاه شخص iام هم X قرار می دیم (مثل شکل). در پایین هم ${100}^{100}$ راس وجود داره که هر راس نمایانگر یه حالت از چینش کلاه هاست. 
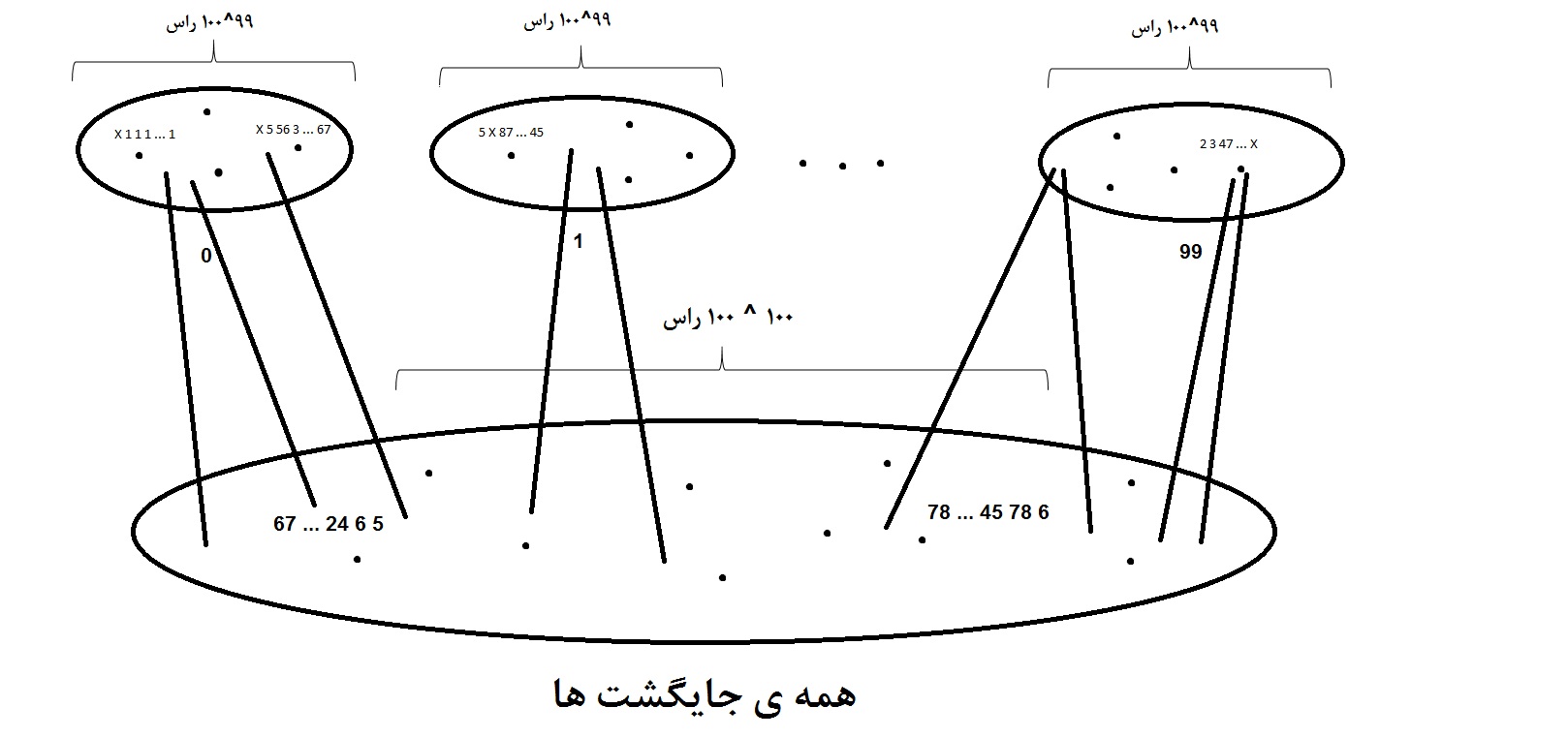هر راس از بالا، به همه ی حالت هایی که ممکنه تو چینش اصلی باشه وصل شده، یعنی همه ی 100 حالتی که X می تونه داشته باشه (1..100). پس درجه ی همه ی راس های بالا 100 هستش. هر راس از پایین هم به 100 راس از بالا وصل شده (همه ی جا های ممکن X در اون چینش). می خوایم اثبات کنیم شرط هال تو این گراف برقراره.
فرض کنیم نباشه، یعنی یه مجموعه ای از راس ها بالا هستن (S) که مجموعه ی همسایه هاشون (N) از خودشون کوچیکتره ($|S| > |N|$). می دونیم از S، تعداد 100S تا یال خارج شده و $|S| > |N|$، پس طبق لانه کبوتری یه راس تو N هست که بیشتر از 100 یال بهش وصل شده که می دونیم این طور نیست. پس شرط هال بر قراره و در نتیجه میشه یه مچینگ تام (Perfect Matching) پیدا کرد. حالا هر کس، از دسته اش تو قسمت بالا اون راسی که مطابق دیدش هست رو پیدا کنه و ببینه یال مچینگش کجا رفته. فرض کنه که شماره کلاه ها همونه و با توجه به اون حالت، شماره کلاهشو بنویسه. اثبات درست بودن:
راس چینش اصلی کلاه ها در قسمت پایین رو در نظر بگیرید. چون مچینگ تام هستش، یکی از 100 یال متصل به این راس توی مچینگ اومده و به یکی از راس های بالا وصل شده. اگر این یال به دسته ی i ام رفته باشه، نفر i ام درست می نویسه، چون که اون چیزی که می بینه همونیه که به یه سر یال وصله و در نتیجه می ره می بینه اون سر یال چه چینشی داره و با توجه به اون شمارشو می نویسه و چون اون سر یال چینش واقعیه، درست می نویسه.
سوالی بود، در خدمتم!