حالت کلی که هیچ من فقط میخام بدونم تو میتونی n=4 رو از رو n=3 بسازی
2015-04-29 04:26:37 -0500 سینا حیدری@سینا حیدری عزیز٬ جهت دسته بندی بهتر سوالات مرحله 2 سوال شما ویرایش شد. لطفا در عنوان سوال توضیح مختصری از محتوای سوال را بیاورید و سال و مرحله را در تگها ذکر کنید.
2015-05-01 07:53:19 -0500 محمدیسلام میدونستید انجمن علمی نخبگان دانشگاه صنعتی شریف مسابقه تخصصی مهارت سنجی برنامه نویسی و داده کاوی گذاشته است آدرس سایتش www.fanavard.com
2015-08-06 07:09:16 -0500 امیر شکریسلام میگم یک سر به سایت www.fanavard.ir بزنید. مسابقات برنامه نویسی شون شروع شده. گواهی رسمی از طرف دانشگاه شریف می ده. 50 تا سکه هم جایزشه
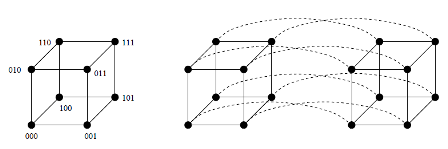
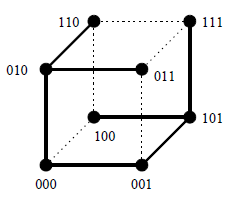
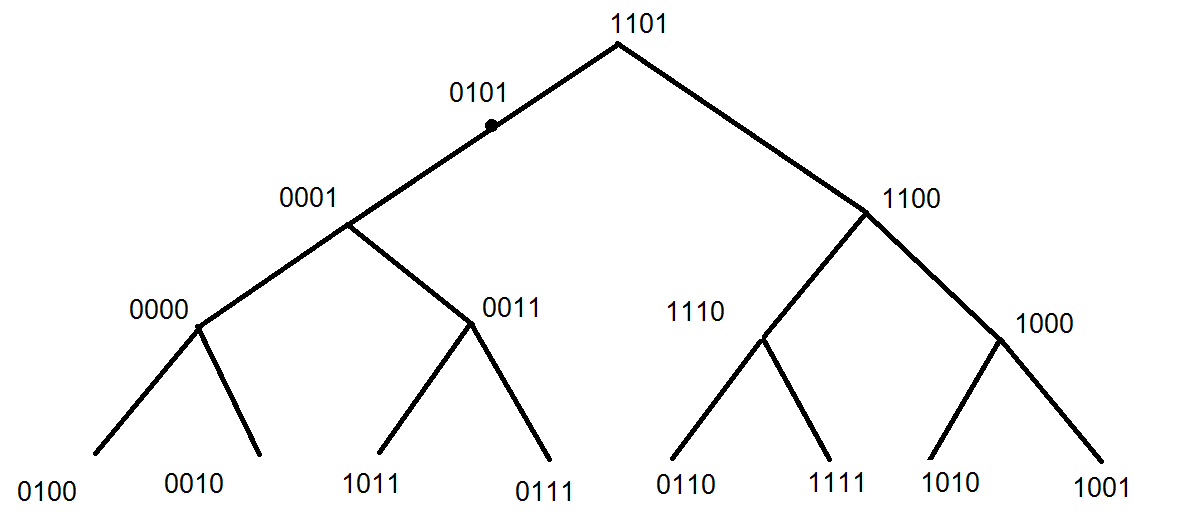
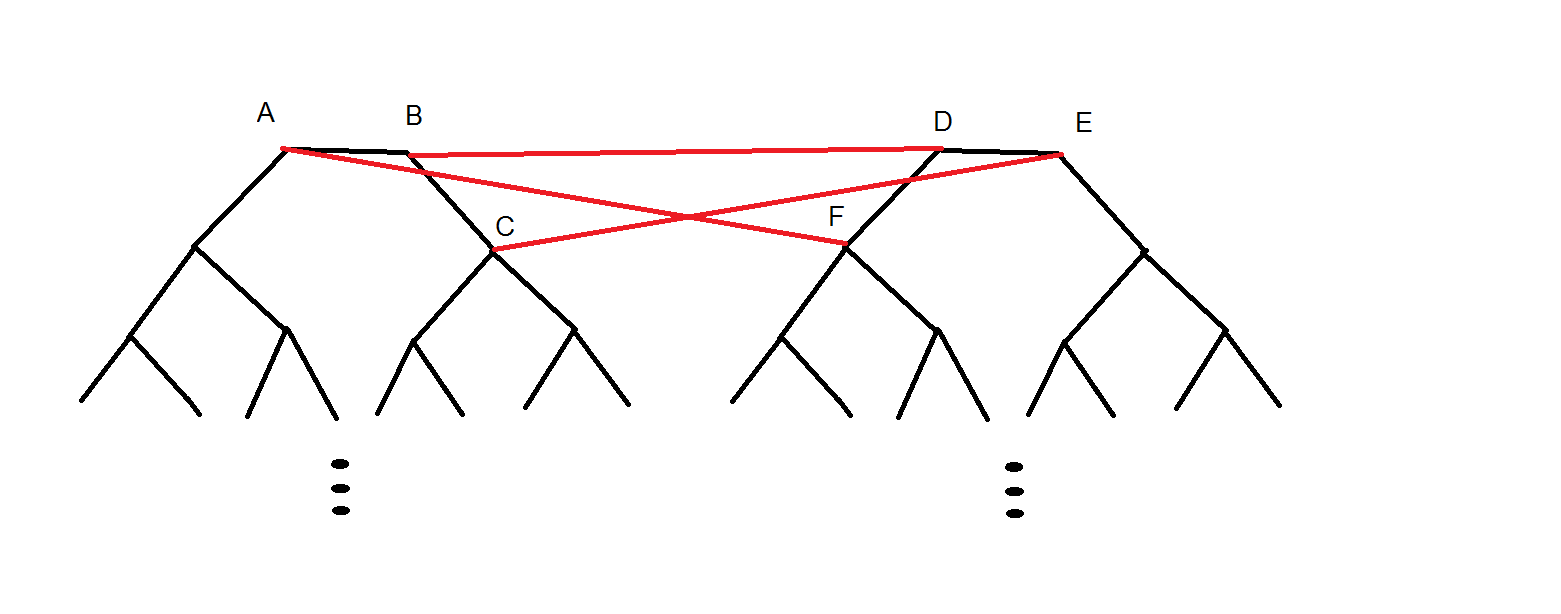
2016-10-26 11:06:51 -0500 امیر شکری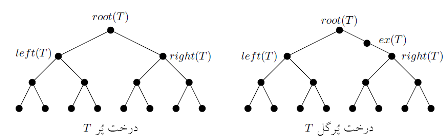 فوق مکعب از درجهی $n$ هم گرافی است با $2^n$ راس، که اگر هر راس آن را با یک عدد $n$ رقمی متمایز در مبنای ۲ نشان دهیم، هر رأس $a_1 a_2 … a_n$ (که $a_i$ یا صفر است و یا ۱) به $n$ رأس دیگر وصل است. دو رأس به هم متصلاند اگر نمایش دودویی آن دو دقیقاً در یک رقم اختلاف داشته باشد. میتوان دید که اگر دو فوق مکعب از درجه ی $n$ را بگیریم و بین هر دو رأس از هر دو فوق مکعب با نمایش بیتی یکسان یک یال اضافه کنیم، یک فوق مکعب از درجه ی $n+1$ به دست می آید. شکل زیر یک فوق مکعب از درجه ی ۳ و فوق مکعب درجه ی ۴ را نشان می دهد.
فوق مکعب از درجهی $n$ هم گرافی است با $2^n$ راس، که اگر هر راس آن را با یک عدد $n$ رقمی متمایز در مبنای ۲ نشان دهیم، هر رأس $a_1 a_2 … a_n$ (که $a_i$ یا صفر است و یا ۱) به $n$ رأس دیگر وصل است. دو رأس به هم متصلاند اگر نمایش دودویی آن دو دقیقاً در یک رقم اختلاف داشته باشد. میتوان دید که اگر دو فوق مکعب از درجه ی $n$ را بگیریم و بین هر دو رأس از هر دو فوق مکعب با نمایش بیتی یکسان یک یال اضافه کنیم، یک فوق مکعب از درجه ی $n+1$ به دست می آید. شکل زیر یک فوق مکعب از درجه ی ۳ و فوق مکعب درجه ی ۴ را نشان می دهد.