راه غیر احتمالاتی این سوال نیاز به خلاقیت داره و این چیزیه که به درد المپیادی میخوره گرچه به طرز عجیبی این سوال یه جوری طرح شده که آخر سر جوابشو باید خوند . کسی هست که این سوالو بدون خوندن جواب حل کرده باشه ؟ منظورم از راه خلاقانه و اصلیشه .
2014-08-21 13:32:04 -0500 سماق دوخود من اول با استقرا حلش کردم . بعدش با روش های احتمالاتیش . راه حل احتمالاتیش هم احتیاج به خلاقیت داره . خیلی از شاگردام هم با دو روش حل کردن . خیلی سوال سختی نیست . بچه ها رو نا امید نکن .
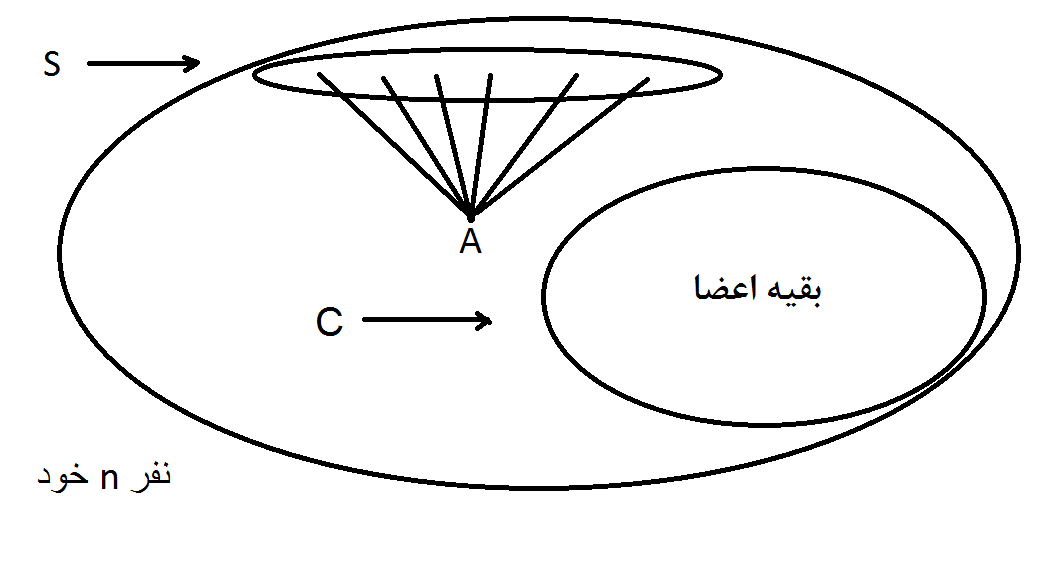
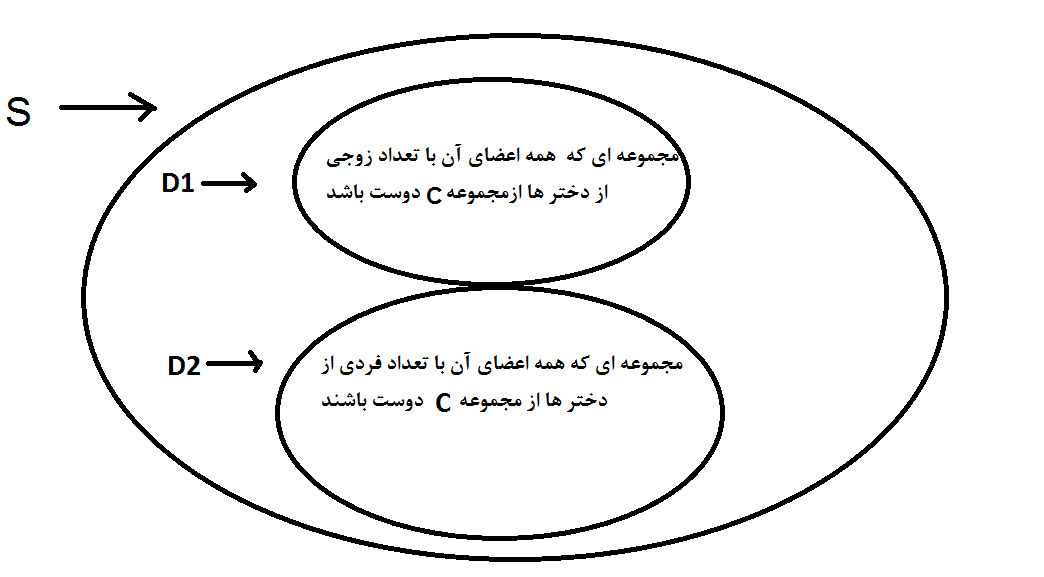
2014-08-22 02:28:56 -0500 حمید کاملیراهنمایی: هر دختر را با احتمال 1/2 انتخاب کنید و در گروه قرار دهید . سپس هر پسر را که با تعداد فردی از دختر ها دوست است را در گروه قرار دهید .
2014-08-28 08:58:15 -0500 حمید کاملی