آمار پرسش:

• پرسیده شده: 2015-04-09 08:11:14 -0500
• مشاهده شده: 1,275 بار
• بروز شده: 2015-04-21 09:46:02 -0500

پرسش‌های مشابه:

سوال۴- خطوط ارتباطی محمد و حسین برای مقابله با تغییر بیت‌های پیغام توسط دشمنانشان

سوال 1- تایید کنید روش مهدی و ایلیا ممکن است به کوچک‌ترین عدد ممکن نرسد

سوال 3- الگوریتمی برای آقای کاف بنویسید که در حداقل زمان بتواند لامپ‌های سالم و نیز سرپیچ‌های سالم را پیدا کند

سوال ۵- انتخاب افراد برای بررسی صندوقچه‌ها

سوال ۶- تعداد جداول اصلاح‌پذیر را به دست آورید

سوال ۷- تعیین سیاست برای تشخیص رنگ کلاه‌ها

سوال ۸- طراحی خیابانهای شهر و محل خانه‌ی شهردار طبق قوانین کشور آنتونیو

سوال 2- قورباغه‌ي پهلوان روی محور اعداد صحیح

سوال ۵- رنگ‌آمیزی پراکنده یک جدول با رنگ‌های سیاه و سفید

سوال ۶- سطل‌ها و توپ‌ها- نشان دهید در هر ۲۰ حرکت متوالی ناچاریم دست کم یک بار به سراغ سطلی با کم‌تر از ۱۰ توپ برویم.

نکاتی در مورد نوشتن پاسخ:

در این قسمت می‌تونی به یک پرسش پاسخ بدی. اگه می‌خوای در مورد پرسش بحث و اظهار نظر کنی از قسمت «ثبت نظر» استفاده کن.
پاسخت رو دقیق و کامل بنویس، از عکس استفاده کن و اگه لازمه به منابع (کتاب یا سایت) ارجاع بده.
اگه پرسش یا پاسخ‌ها مفید هستند حتما بهشون رای بده تا پرسش‌ها و پاسخ‌های خوب مشخص بشن.

استفاده از ویرایشگر:

توی قسمت پیش‌نمایش می‌تونی ببینی متنی که نوشتی چجوری روی سایت دیده میشه.
خیلی مهم: برای اینکه به خط بعد بری باید دوتا Enter بزنی.
می‌تونی از تگ‌های معمولی و ساده‌ی html هم استفاده کنی.
با دکمه‌هایی که بالای ویرایش‌گر قرار دارند کلی کار می‌شه کرد. از عکس‌گذاشتن بگیر تا لیست شماره‌دار. حتما امتحان‌شون کن.

علائم ریاضی:

برای نوشتن علائم ریاضی می‌تونی از Mathjax استفاده کنی. راهنمای Mathjax رو از سایت math.stackexchange بخون.
برای نوشتن عبارت ریاضی وسط جمله، اون عبارت رو بین دوتا $ قرار بده.
برای نوشتن عبارت ریاضی تو یه خط جدید اون رو بین دوتا $$ قرار بده.

سوال2- پوشاندن کف یک اتاق مستطیل شکل با تعدادی متناهی فرش طبق یک نقشه‌ی قابل قبول

3

لینک برای مشاهده ی بهتر سوال

کف یک اتاق مستطیل شکل را می‌خواهیم با تعدادی متناهی فرش بپوشانیم. تمام فرش‌ها مستطیل شکل‌اند و ابعادی حقیقی دارند. یک نقشه‌ی قابل قبول٬ نحوه‌ی قرار گرفتن هر فرش در اتاق را نشان می‌دهد به طوری که هر نقطه‌ی اتاق دقیقاً توسط یک فرش پوشانده شده باشد؛ یعنی فرش‌ها روی هم قرار نگرفته‌اند و هیچ جای اتاق خالی نیست. می‌دانیم در هر نقشه‌ی قابل قبول٬ ضلع‌های هر فرش موازی اضلاع اتاق خواهد بود.

یک نقشه‌ی قابل قبول داده شده است. می‌خواهیم ترتیب پهن کردن فرش‌ها را مشخص کنیم٬ یعنی به هر یک از فرش‌ها شماره‌ای اختصاص دهیم که مشخص کند آن فرش٬ چندمین فرشی است که باید پهن شود. یک ترتیب را خوب می‌نامیم اگر زمانی که طبق آن ترتیب فرشی پهن می‌شود٬ ضلع‌های پایین و چپ آن فرش٬ یا دیوار باشد و یا هیچ قسمت فرش نشده‌ای نداشته باشد.

مثلاً در زیر شکل (۱) یک نقشه‌ی قابل قبول است٬ و شکل (۲) آن یک ترتیب غیر خوب را نشان می‌دهد٬ چرا که هنگام اضافه شدن فرش شماره‌ی ۳ قسمتی از پایین این فرش هنوز پوشانده نشده است٬ که بعداً توسط فرش ۴ پوشانده می‌شود. شکل (۳) یک ترتیب خوب را نشان می‌دهد. ثابت کنید که به ازای هر نقشه‌ی قابل قبول٬ یک ترتیب خوب وجود دارد.

مرحله۲ کلاس-دوم ۱۳۸۵

2015-04-09 08:11:14 -0500

آرپا 947 ● 13 ● 15 ● 31

پاک‌کردن   ویرایش سوال

نظرات

امیررضای عزیز٬ لطفا برای قرار دادن سوال‌های سالهای گذشته شماره سوال و شرح مختصری از آن را در عنوان بنویس و سال و مرحله را در برچسب‌ها بیار

2015-04-21 09:47:56 -0500 محمدی

سلام میدونستید انجمن علمی نخبگان دانشگاه صنعتی شریف مسابقه تخصصی مهارت سنجی برنامه نویسی و داده کاوی گذاشته است آدرس سایتش www.fanavard.com

2015-08-06 07:15:37 -0500 امیر شکری

سلام میگم یک سر به سایت www.fanavard.ir بزنید. مسابقات برنامه نویسی شون شروع شده. گواهی رسمی از طرف دانشگاه شریف می ده. 50 تا سکه هم جایزشه

2016-10-26 11:11:48 -0500 امیر شکری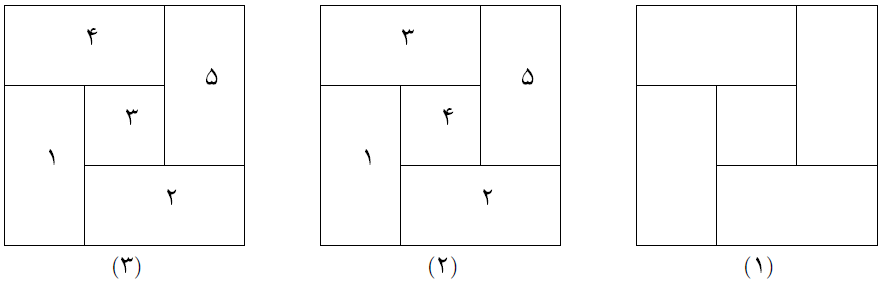

4

یه نقشه ی قابل قبول رو در نظر می گیریم و از رو ی اون به این صورت یه گراف جهت دار می سازیم:به ازای هر فرش یه راس می زاریم از راس u به راس v یال جهت دار می دیم اگر و تنها اگر فرش u سمت چپ و مجاور v یا پایین و مجاور v باشه حالا گراف یه دگه اثباتش هم به این صورته که فرض کنیم یه دور جهت دار داشته باشیم اگر از یه راس شروع می کنیم و در آخر مسیر دوباره به این راس می رسیم که این یعنی یه فرش پایین یا چپ خودشه که امکان نداره.حالا یه توپولوژیکال سورت رو این DAG می زینم و از شماره ی راس ها رو به فرش های متناظرشون می دیم واضحه که حکم مسئله برقراره

2015-04-09 08:59:22 -0500

عطا 1110 ● 7 ● 12 ● 29

پاک‌کردن   ویرایش پاسخ

نظرات

+1 منم همین راه رفتم :د !

2015-04-09 10:26:32 -0500 چشمک

الان همین توضیح برا جواب این سوال کافیه ؟ درباره توپوژیکال سورت توضیح خاصی نباید بدیم ؟!

2016-04-01 05:51:18 -0500 میم عین

1

استقرا میزنیم
فرض استقرا. به ازای هر تعداد و هر ارایش مستطیل های متصل به هم یک ترتیب خوب وجود دارد. (دقت کنید نه فقط به ازای یک مستطیل که به چند تا مستطیل تقسیم شده، در اصل فرض استقرا رو قوی کردم)
پایه ۱ که بدیهیه به ازای n-1 فرض میکنیم برقرار باشه حالا تو n چپ ترین و پایین ترین خونه رو برابر ۱ و بقیه بر اساس فرض استقرا از ۲ میزاریم(چون شکل ها رو صفحس چپ ترین پایین ترین داره)

2015-04-09 09:11:48 -0500

کامیاب 365 ● 1 ● 1 ● 8

پاک‌کردن   ویرایش پاسخ

نظرات

من هم همین راهو رفتم فقط باید تمام گوشه های سمت چپ شکل رو از پایین به بالا بری و بگی اگه این نشد بالاییش میشه و اگه بالاییش نشد بالاییش و ... تا بری برسی به بالای شکل و اون دیگه میشه.

2016-04-17 13:34:56 -0500 ادن هازارد